Исследование свойств картографической проекции,заданной определённой системой координат, страница 2

Вывод: исследуемая проекция по виду картографической сетки является цилиндрической, по характеру искажений - произвольной.

Исследование второй проекци

Пусть картографическая проекция задана  уравнением следующего вида:

X=R sin φ

У=R λ

1.  Определяем вид меридианов и параллелей.

В первом уравнении проекция X является функцией только широты φ. Следовательно, уравнение X=R sin φ при φ=const  представляет собой  уравнение параллелей, изображающихся  прямыми параллельными линиями. Во втором уравнении Y является функцией только долготы λ. Следовательно, уравнение  Y=Rλ, при λ=const представляет собой уравнение меридианов, так же изображающихся прямыми параллельными линиями.

Делаем вывод о том, что исследуемая проекция – цилиндрическая.

2. Построение сетки.

а) Определяем масштаб построения сетки.

С учётом заданного формата чертежей бумаги для построения картографической сетки и вытянутости изображения земной поверхности в цилиндрической проекции с запада на восток масштаб построения проекции стоит определять выражением:

μ_о=21/2πR

где 21 см-длина экватора на плоскости;

2πR-длина экватора на поверхности сферы.

R=64∙10⁷ см

μ_о=26/6,28∙64∙10⁷=1/157 000 000

Для удобства в расчётах координат x,y масштаб построения следует округлить,а именно принять его равным  :

μ_о=1/160 000 000

б) Для построения параллелей, с учётом уравнения параллелей вычисляем:

х=R∙sin∙φ∙μ_o

Вычисляем абсцисс для будущего эскиза картографической сетки, делаем до 90  параллели.

Результаты вычислений x_i приведены в (таблице №1):

Таблица 1

Абcциссы x_i

φº	Хi
0	0,00
30	2,00
60	3,46
90	4,00

Из таблицы видно, что экватор совпадает с осью Y. Последовательно откладывая от оси Y расстояния х₂ , х₃  ,х₄  ,находим положение параллелей 30º,60º,90º.

в) Строим меридианы, используя уравнение меридианов:

у=Rλ

Учитывая, что λ не выходит за знак какой-либо функции, можно сделать вывод о том, что расстояние между меридианами на каждой конкретной параллели есть величина постоянная. Поэтому для построения меридианов достаточно принять λ=30º(меняя φ то 0º до 90º).Вычисления для построения меридианов приведены в таблице 2:

Таблица 2

Ординаты У_i

λ0	λ	уi(см)
0	0,00	0
30	0,523	2,08
60	1,046	4,18
90	1,570	6,28

Средний меридиан λ=0⁰ будет совпадать с осью Х. Полученное значение у=2,08 при λ=30⁰ откладываем 6 раз на восток и на запад по оси Y и Х до 180⁰ с западной частотой построения сетки.

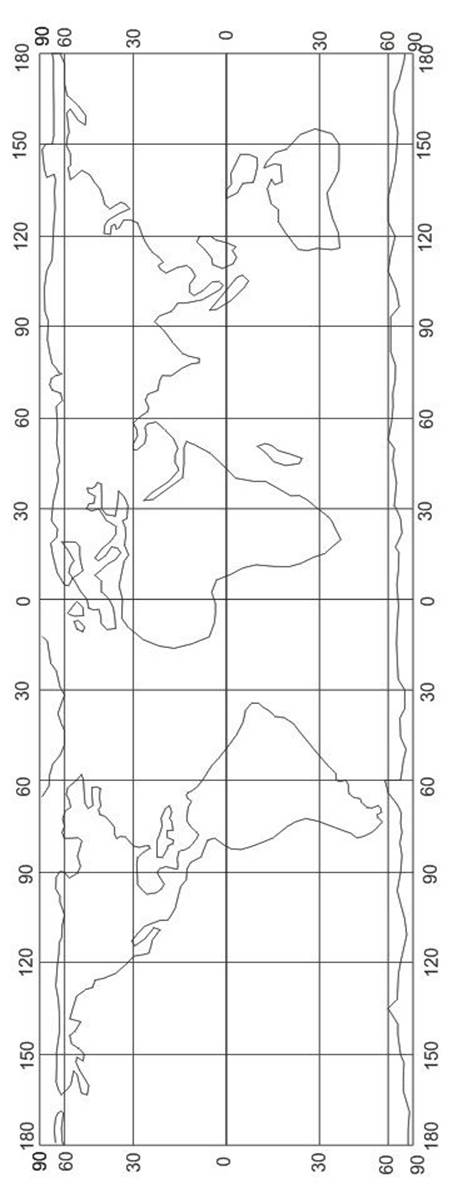
3.На построенную картографическую сетку наносим  рисовкой по клеткам необходимые контуры материков, используя географические атласы.

Определяем свойства картографической проекции.

а) Находим частные производные по заданным уравнениям:

Х_φ=R∙cosφ

X_λ=0

Y_φ=0

Y_λ=R

б) Определяем Гауссовы коэффициенты по уравнениям:

E= X_φ²+Y_φ²=R²cos²φ

G= X_λ²+Y_λ²=R²

F=X_φX_λ+Y _φY_λ=0

H=X_φY_λ-X_λY_φ=R²∙cosφ

в) Находим в общем виде выражения для характеристик проекции по формулам:

m=√E/R=cosφ

n=√G/R∙cosφ=√R²/Rcosφ=1/cosφ

sinϴ=H/√EG=(R²cosφ)/√(R²cos²φR² )= 1

p=m∙sinϴ=cosφ∙(1/cosφ)∙1=1

a=1/cosφ

b=cosφ

sin ω/2=(a-b)/(a+b)=(cosφ-1/cosφ)/(cosφ +1/cosφ)

tg γ= -Y_φ/X_φ=0∙Rcosφ=0

4.Вычисляем величины искажений в узловых точках  сетки (таблица №3):

Таблица 3

Вывод: исследуемая проекция по виду картографической сетки является цилиндрической, по характеру искажений - произвольной.