Операции над матрицами обучение нейронной сети по правилу Хебба. Результат выполнения оператора, функции

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И УПРАВЛЕНИЯ

кафедра прикладных информационных технологий

Институт  Прикладной информатики

Учебная дисциплина:  Информационные технологии

ЛАБОРАТОРНАЯ РАБОТА № 4

ОПЕРАЦИИ НАД МАТРИЦАМИ

ОБУЧЕНИЕ НЕЙРОННОЙ СЕТИ ПО ПРАВИЛУ ХЕББА

Дисциплина:  Информационные технологии

Номер группы: 1741

Выполнила: 

Номер варианта: 10

Проверила:

Дата регистрации на кафедре: «__»___________2013 г.

Новосибирск – 2013

Задание1. Операции над матрицами. Поэлементное умножение матриц.

>> a = [11 25 34];

>> b = [31 29 18];

>> c=a.*b;

>> A=ones(3)                       

A =  1     1     1

1     1     1

1     1     1

B= [1 2 9; 42 15 16; 27 38 49]

B =

1     2     9

42    15    16

27    38    49

>> C=A.*B;                        

>> D=A./B;                         

>> E=A.^3;                          

>> a = [1 6 3 4];

>> [v, i] = max (a);

>> v = max(a);       

>> A=[8 9 11; 3 7 1; 3 1 9];

>> S1=sum(A);        

>> S1=sum(sum(A));

>>  [v, i] = max (a)

v = 6

i =2

S1=sum(A)

S1 =  14    17    21

S1=sum(sum(A))

S1 = 52

Сортировкаэлементовматрицы

>> a=[11 -8 5 48 56 98];

b2=sort(a,'descend');

b3=sort(a,'ascend');

disp (a)

disp (b2)            

disp (b3)             

11    -8     5    48    56    98

98    56    48    11     5    -8

-8     5    11    48    56    98

>> c = [4 8 9 4 8 9 48]

d1=find (c ==48)  

d2=find (c~=48)  

d3=find (c>4)      

Нахождение определённого элемента в векторе или матрице выполняется при помощи функции find

c = 4     8     9     4     8     9    48

d1 =7

d2 = 1     2     3     4     5     6

d3 =2     3     5     6     7

Вычисление среднего арифметического в векторе производится вызовом функции mean (а)

>> a = [4 9 5 6 98];

>> c1= mean(a);    

Нахождение среднего арифметического в матрице размерностью 3*3                                                          

>> A = [48 45 14; 23 56 41; 3 4 9];

>> M1 = mean (A);                                             

>> M2 = mean (mean (M1))                                 

M2 =  27

Нахождение суммы элементов массива с использованием цикла while

Пример 1.

>> s=0;

>> i=1;

>> while i<=40

s=s+i;

i=i+1;

end

>> disp(s)  820

Найтисуммуэлементовмассива

Пример 2.

>> s=0;

>> a=[1 5 9 12 13 15 48];

>> i=0;

>> while i<length(a)

i=i+1;

s=s+a(i);

end

>> disp(s)103

Необходимо подчитать сумму элементов в матрице-векторе с условием пока счетчик доходит до 40 или превысит его значение.

>> s=0;

>> i=1;

>> while i<=40 & s<=700      

s=s+i;               

i=i+1;             

end    

>> disp(s) 703

Найти максимальное значение элемента в векторе

>> a = [5 8 11 45 89 45]

a = 5     8    11    45    89    45

>> m = a (1);

>> for i=1:length(a)

if m < a (i)

m = a (i);

end  end

>> disp (m)  89

Задание 2. Обучение нейронных сетей по правилу Хебба.

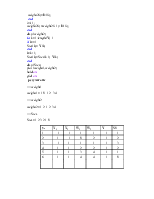
Исходные данные и результаты обучения сети по правилу Хебба

Постановка задачи: необходимо реализовать обучение нейронной сети  по правилу Хебба с учителем, используя при этом биполярную кодировку двоичных сигналов.

Общее количество входных образов, участвующих в обучении сети составляет N=10.