Операции над матрицами обучение нейронной сети по правилу Хебба. Результат выполнения оператора, функции, страница 2

Исходные данные и результаты обучения сети по правилу Хебба

Согласно правилу обучения для случая с тремя нейронами и одним выходом подстройка весовых коэффициентов производятся по формулам:

W1₁ (t+1)=W₁₁ (t)+X₁Y.

W2₁(t+1)=W₂₁(t)+X₂Y.

S₀(t+1)=S₀(t)-Y

При этом начальные значения синаптических весов принимаются равными нулю, т.е. W1₁⁽⁰⁾=0, W2₁⁽⁰⁾=0,  S₀(0)=0.

Простейшая математическая модель  обучения Хебба (правило умножения активности)  записывается в виде :

W_ij(t+1)=W_ij(t)+ɳx_iy_j,

W_ij=W_ij(t+1)-W_ijj(t)=ɳx_iy_j

Где ɳ- коэффициент скорости обучения нейронной сети , задается в интервале (0,1); i=1,2,3,…N,j=1,2,3,…M

Правило Хебба может применяться для нейронных сетей различных типов с разными функциями активации.  Ограничение применения правила обучения нейронных сетей по Хеббу заключается в том, что веса могут принимать произвольно большие значения , т.к. в каждом цикле происходит суммирование текущего значения с его приращением W_ij.

Гипотеза ковариации правила Хебба. Согласно гипотезе предсинаптические и постсинаптические  сигналы заменяются отклонениями от этих сигналов от средних значений  на данном отрезке времени:

W_ij=ɳ(x_ii-x)(y_i-y),

Где x,y,- усредненные значения предсинаптического и постсинаптического  сигналов.

Способом модификации весов  привила Хебба является уточнение веса, уменьшенного на коэффициент забывания:

W_ij(t+1)=W_ij(t)(1-y)+W_ij(t)

Где y-коэффициент забывания (0,1).

При  больших значениях коэффициента забывания (Y) нейрон «забывает» значительную часть того , чему обучился нейрон в прошлом, поэтому  при обучении сетей коэффициенту  присваиваются небольшие значения в процентах от коэффициента обучения(ɳ).

X=[-1 -1;1 -1;-1 1;1 1;1 1;1 1];

Y=[-1;-1;-1;1;1;1];

koeff=1

weight1=zeros(6,1);

weight2=zeros(6,1);

Sres=zeros(6,1);

C=X(:,1)

C1=C.*Y*koeff;

for i=1:length(X)-1

if i==1

weight1(i)=C1(i);

end

i=i+1;

weight1(i)=weight1(i-1)+C1(i);

end

disp (weight1)

D=X(:,2);

D1=D.*Y*koeff

for i=1:length(X)-1

if i==1

weight2(i)=D1(i);

end

i=i+1;

weight2(i)=weight2(i-1)+D1(i);

end

disp (weight2)

for k=1:length(Y)-1

if k==1

Sres(k)=-Y(k)

end

k=k+1;

Sres(k)=Sres(k-1)-Y(k)

end

disp (Sres)

plot (weight1,weight2)

hold on

grid on

результаты

>> weight1

weight1 = 1 0  1 2  3 4

>> weight2

weight2 =1 2  1  2 3 4

>> Sres

Sres =1 2 3 2 1 0

№	X1	X2	W1	W2	Y	S0
1	-1	-1	1	1	-1	1
2	1	-1	0	2	-1	2
3	-1	1	1	1	-1	3
4	1	1	2	2	1	2
5	1	1	3	4	1	1
6	1	1	4	4	1	0

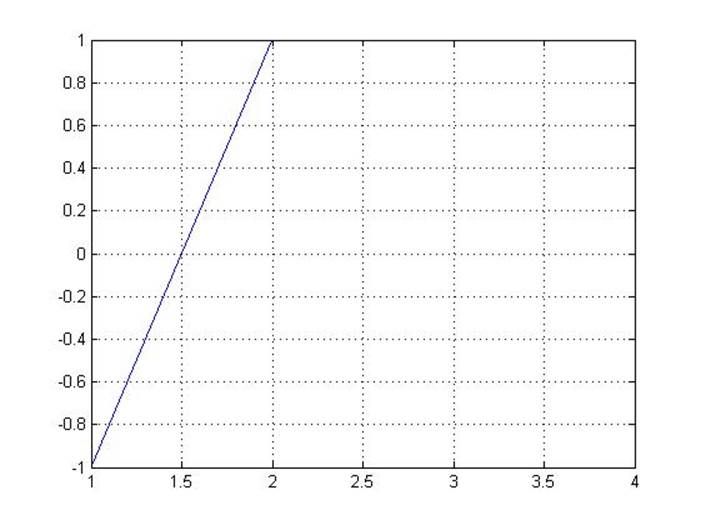
Рисунок 1 - График зависимости изменения синаптического веса от постсинаптического сигнала

Задание 3. Самостоятельно написать программный код для обучения нейронной сети с модификацией правила Хебба.

X=[-1 -1; 1 -1; -1 1; 1 1; 1 1; 1 1];     

Y=[-1;-1;-1;1;1; 1];            

koeff=1;

W1=zeros(6,1);               

W2=zeros(6,1);               

Sres=zeros(6,1);             

Xsr=mean(X)           

Ysr=mean(Y);       

Xsr1=Xsr(1);          

Xsr2=Xsr(2);         

A=X(:,1)-Xsr1; 

B=X(:,2)-Xsr(2);

F=Y(:)-Ysr;

C1=A.*F*koeff;                 

D1=B.*F*koeff;

for i=1:length(X)-1       

if i==1

W1(i)=C1(i);

end

i=i+1;

W1(i)=W1(i-1)+koeff*C1(i);

end%disp(W1)

D=X(:,2);

D1=D.*Y;

for i=1:length(X)-1       

if i==1

W2(i)=D1(i);

end

i=i+1;

W2(i)=W2(i-1)+koeff*D1(i);

end%disp(W2)

for k=1:length(F)-1

if k==1

Sres=-F(k);

end

k=k+1;

Sres(k)=Sres(k-1)-F(k);

end%disp(Sres)

Расчет в таблицу

W1=1.3333   0.833    1.8333  2.333   2.8333 3.3333

W2 =1.0000  1.7500 1.0000  1.7500   2.5000 3.2500

Sres =   1     2     3     2     1     0

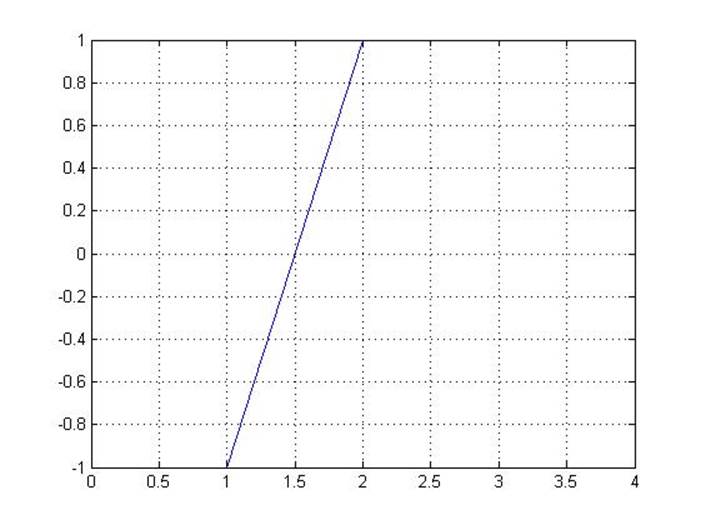
Рисунок 2 - График зависимости изменения синаптического веса от постсинаптического сигнала