Многослойный персептрон. Понятия и структура многослойной нейронной сети. Алгоритм обратного распространения ошибки

НовосибирскИЙ государственнЫЙ УНИВЕРСИТЕТ экономики и управления

кафедра прикладных информационных технологий

Институт  Прикладной информатики

Учебная дисциплина:  Информационные технологии

                                 ЛАБОРАТОРНАЯ РАБОТА № 7

                                        Многослойный персептрон

Дисциплина:Информационные технологии

Номер группы: 1741

Выполнила:

Номер варианта: 17

Проверила:

Дата регистрации на кафедре: « »    декабря    2013 г.

                                          Теория:     Многослойный персептрон

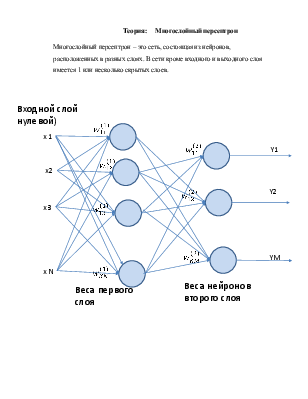
Многослойный персептрон – это сеть, состоящая из нейронов, расположенных в разных слоях. В сети кроме входного и выходного слоя имеется 1 или несколько скрытых слоев.

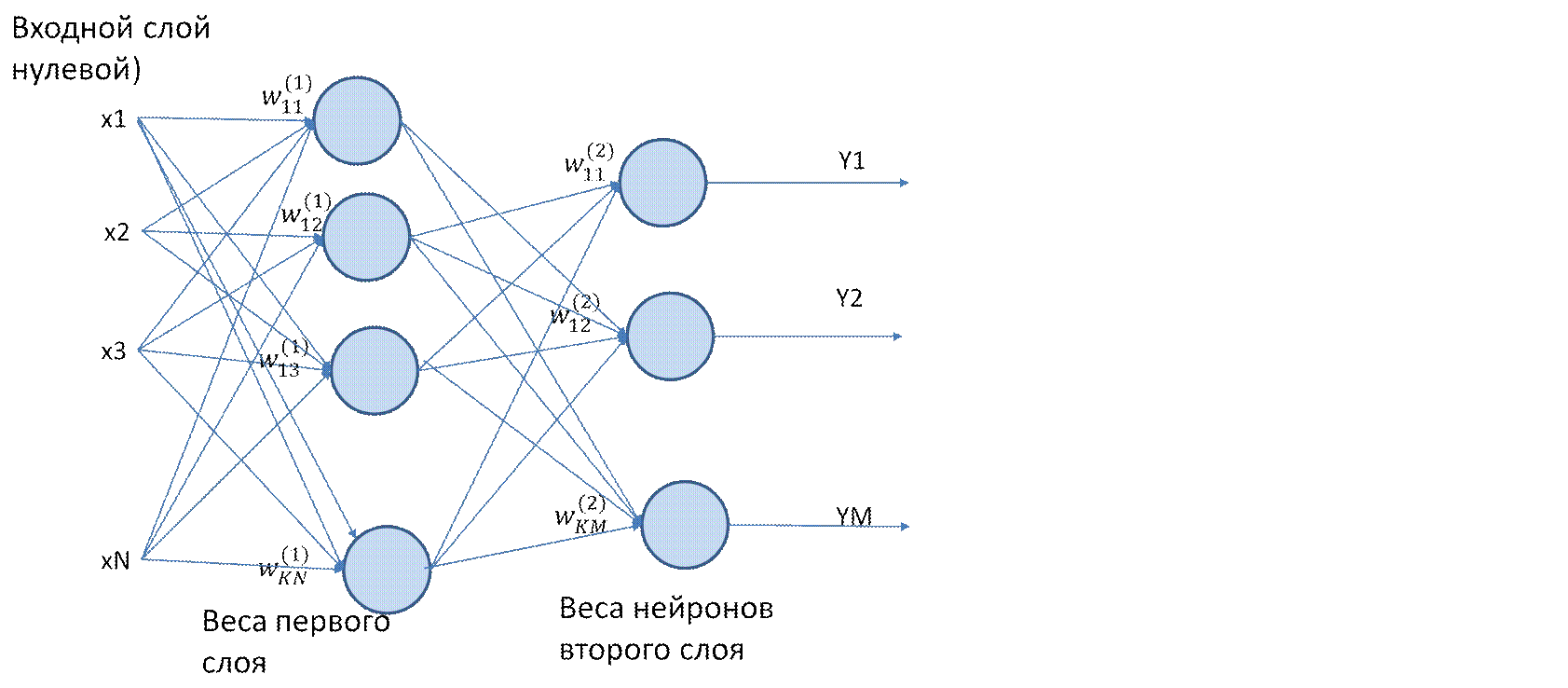
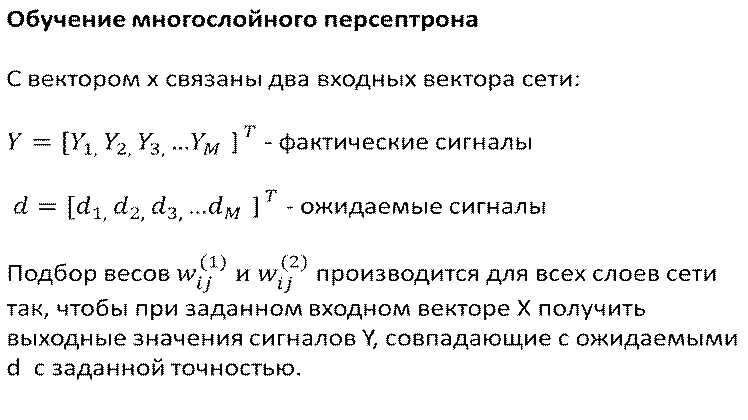
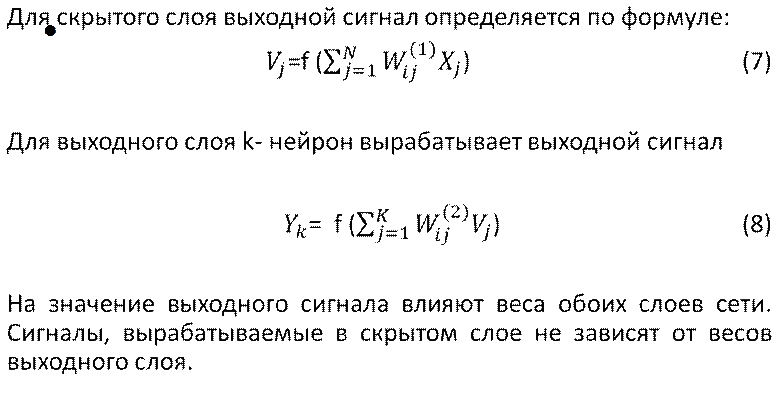
Многослойный персептрон

Содержание:

1)Понятия и структура многослойной нейронной сети

2)Алгоритм обратного распространения ошибки.

3)Программный код обучения нейронной сети, алгоритмом обратного распространения ошибки.

4)Выводы.

1-очищаем графическое окно.

2-задаём сигмоидальную функцию активации: f(s)=1/1+e^-as

3-вычисляем её производную.

4-задаём массив входным данным-(х)

5-задаём массив обучающей выборки.

6,7 и 8 строки - настраиваем параметры нейронной сети начальные весовые коэффициенты случайным образом.

9-задаём количество циклов обучения

10-задаём размерность, для вычисления ошибки обучения

11- задаём размерность, для вычисления ошибки обучения от 1 до числе итераций

12-рассчитываем величину ошибки в прямом ходе, для каждого нейрона

13-выбирем текущий объект из матрицы входных данных

14,15 и 16-вычисляем величину ошибки в прямом коде, для каждого нейрона

17-расчитываем выход сети

18,19 и 20-расчитываем величину ошибки в обратном коде

21,22 и 23-расчитываем весовые коэффициенты

24-расчитываем величину ошибки, согласно алгоритму обратного распространения

Алгоритм обратного распространения ошибки

clf

S=@(z)1./(1+exp(-z));

Sd=@(z) S(z).*(1-S(z));

X=[0 0;1 1;0 1;1 0]

Y=[0 0 1 1]'

w1=rand([3 1])

w2=rand([3 1])

w3=rand([3 1])

iteration=100;

Er=zeros([1 iteration]);

for j=1:iteration

for i=1:size(X,1)

x=X(i,:);

v1=[1 x]*w1;

v2=[1 x]*w2;

v3=[1 S(v1) S(v2)]*w3;

out=S(v3);

e3=out-Y(i);

e1=w3(2)*e3*Sd(v3);

e2=w3(3)*e3*Sd(v3);

w3=w3-e3.*Sd(v3).*[1 S(v1) S(v2)]';

w1=w1-e1.*Sd(v1).*[1 x]';

w2=w2-e2.*Sd(v2).*[1 x]';

end;

Er(j)=abs(e3);

end;

NS=@(x)S([S(x*w1(2:end)+w1(1).*ones([size(x,1)1])) S(x*w2(2:end)+w2(1).*ones([size(x,1)1]))]*w3(2:end)+w3(1).*ones([size(x,1)1]))

x=-0.5:0.05:1.5;

y=-0.5:0.05:1.5;

[x y]=meshgrid(x,y);

z=NS([x(:) y(:)]);

z=reshape(z, size(x));

mesh(x,y,z)

hold on

scatter3(X(:,1),X(:,2),Y,50,Y)

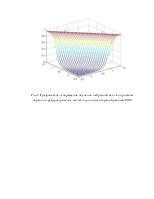
Получается рисунок (1)

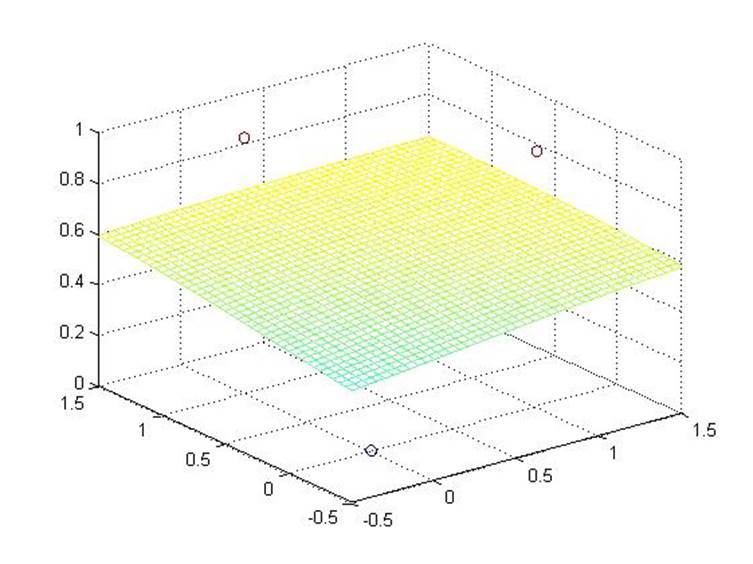
Рис.1. Графическое отображение обучение нейронной сети алгоритмом обратного распространения ошибки при числе итераций равным 100

Меняем значение в коде «iteration=100;» на  «iteration=1000;»

и получается рисунок (2)

Рис.2. Графическое отображение обучение нейронной сети алгоритмом обратного распространения ошибки при числе итераций равным 1000