Лабораторная №3
Интерполирование и аппроксимация функции.
Полином пятой степени.Задание1
polyfit
p=polyfit(x,y,n)
clc-очищаем командное окно
global var1; -объявляем глобальные переменные
global var2; -объявляем глобальные переменные
var1 = [1.67 2.20; 1.82 3.0; 2.0 4.0;2.07 4.5;2.1 5.0;2.11 6.20;2.13 8.0] – присваиваем значение переменной
var2=[1.94 3.0; 2.13 4.0;2.25 6.0;2.32 7.0;2.4 11.0;2.26 15.0] x2 = var1(:,1); - формирование вектора независимой переменной
y2= var1(:,2);-формирование вектора зависимой переменной
P2 = polyfit(x2,y2,5)-расчет коэффициента полинома 5 степени
F2= polyval(P2,x2) – вычисление значений полинома в заданных точках
graph1=plot(x2,y2,’k*’,x2,F2,’k’); -строим график
set(graph1,’LineWidth’,3); - изменяем толщину графика
Вматлабе:
>> global var1;
>> global var2;
>> var1 = [1.67 2.20; 1.82 3.0; 2.0 4.0;2.07 4.5;2.1 5.0;2.11 6.20;2.13 8.0]
var1 =
1.6700 2.2000
1.8200 3.0000
2.0000 4.0000
2.0700 4.5000
2.1000 5.0000
2.1100 6.2000
2.1300 8.0000
>> var2=[1.94 3.0; 2.13 4.0;2.25 6.0;2.32 7.0;2.4 11.0;2.26 15.0]
var2 =
1.9400 3.0000
2.1300 4.0000
2.2500 6.0000
2.3200 7.0000
2.4000 11.0000
2.2600 15.0000
>> x2 = var1(:,1);
>> y2= var1(:,2);
>> P2 = polyfit(x2,y2,5)
P2 =
1.0e+006 *
0.0357 -0.3427 1.3150 -2.5190 2.4085 -0.9195
>> F2= polyval(P2,x2)
F2 =
2.2000
2.9998
4.0053
4.4377
5.2897
5.9205
8.0470
>> graph1=plot(x2,y2,'k*',x2,F2,'k');
>> set(graph1,'LineWidth',3);
Полином третей степени. Задание 2
Формирование вектора не зависимой переменной, потом не зависимой переменной
Задание2
y=polyval(p,s)
p(x)=3x2 +2x+x
в точке x=2,5
p=[3 2 1]
y=polyval(p,2.5)
% y=24.75
Задание1
x3= var2(:,1);
y3= var2(:,2);
P3 = polyfit(x3,y3,3)
F3= polyval(P3,x3)
graph2=plot(x3,y3,’r-’,x3,F3,’k’);
set(graph2,’LineWidth’,2);
xlabel(‘переменная x’);
ylabel(‘функция’);
hold on
grid on
В матлабе:
Задание1
Интерполирование данных с помощью степенных полиномов
x3= var2(:,1);
y3= var2(:,2);
P3 = polyfit(x3,y3,3)
F3= polyval(P3,x3)
P3 =
1.0e+003 *
-0.3623 2.3679 -5.1232 3.6755
F3 =
2.9092
4.7179
8.7630
10.3293
10.2297
9.0508
>> graph2=plot(x3,y3,'r-',x3,F3,'k');
>> set(graph2,'LineWidth',2);
>> xlabel('переменная x');
>> ylabel('функция');
>> hold on
grid on
Задание2
Вычислить значения полинома в заданной точке
>> p=[4 3 0.5 1]
p =
4.0000 3.0000 0.5000 1.0000
>> y=polyval(p,1.6)
y = 25.8640
>> p=[3 2 1]
y=polyval(p,2.5)
% y=24.75
p =
3 2 1
y =
24.7500
Задание3
Интерполяция линейная и интерполяция сплайнами
Сплаинт
y=cos(x) по 9 точкам синтаксис функции interp
y= interp1(x,y,’method’)
nearest – по соседним точкам
linear – линейная
spline- кубичискими сплайнами
cubic-кубический полином
x=0:9; - задоем в интервали от нуля до 9
y=cos(x);
xi=linspace(0,9,100);-генерирум вектор страку из 100 элементов от 0 до 9
yi1=interp1(x,y,xi); - построение ленейного полинома
yi2=interp1(x,y,xi,’spline’);- построение сплаинт полиномов
plot(xi,[yi1;yi2]);- построение графика
clc
clf
x=0:10;
y=sin(x)
xi=0:0.25:10;
yi=spline(x,y,xi);
plot(x,y,’k’,xi,yi,’r’);
grid on
clc
clf
x=0:12;
y=exp(x) %y=e^x
xi=0:0.8:15
yi=spline(x,y,xi);
plot(x,y,’k’,xi,yi,’r’);
grid on
Задание 3
>> x=0:0.12:12;
>> y=cos(x);
>> xi=0:0.12:12;
>> yi=spline(x,y,xi);
>> plot(x,y,'k',xi,yi,'r');
grid on
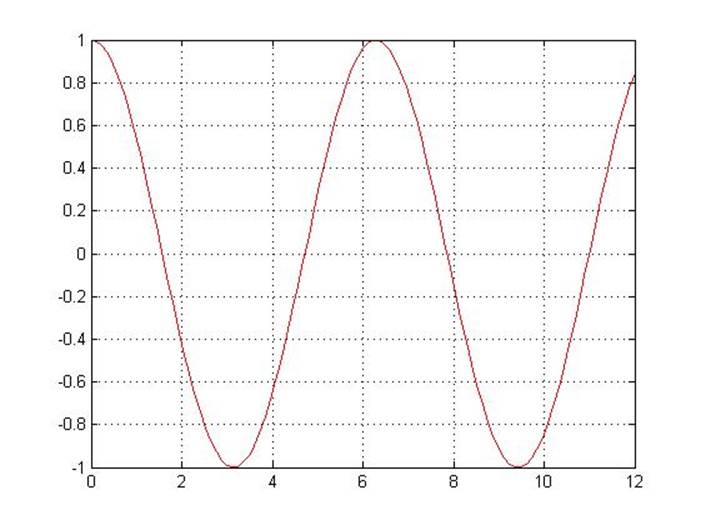
>> x=0:0.12:12;
>> y=sin(x);
>> xi=0:0.12:12;
>> yi=spline(x,y,xi);
>> plot(x,y,'k',xi,yi,'r');
grid on
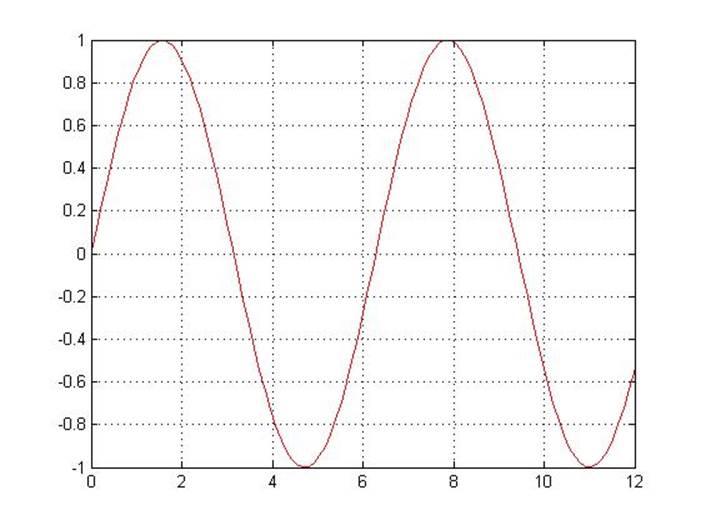
>> x=0:0.12:12;
>> y=tan(x);
>> xi=0:0.12:12;
>> yi=spline(x,y,xi);
>> plot(x,y,'k',xi,yi,'r');
grid on
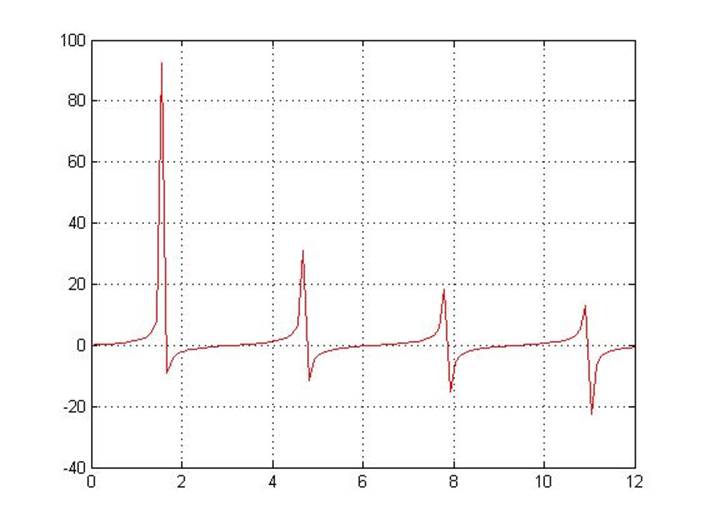
Задание 4 Интерполяция табличных данных
|
X |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
|
Y |
-2.99 |
-2.96 |
-2.91 |
-2.84 |
-2.75 |
-2.64 |
-2.51 |
-2.36 |
-2.19 |
clc
clf
x=[0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]
y=[-2.99 -2.96 -2.91 -2.84 -2.75 -2.64 -2.51 -2.36 -2.19]
xi=[x(1):0.1:x(length(x))];
ynear=interp1(x,y,’nearest’);
yline= interp1(x,y,’spline’);
subplot(2,2,1);
>> plot(x,y,'k*');
>> title('исходные данные');
>> subplot(2,2,2);
>> plot(x,y,'k*',xi,ynear,'k-');
>> title('По соседним значениям');
>> subplot(2,2,3);
>> plot(x,y,'k*',xi,yline,'k-');
>> title('кубический сплаинт');
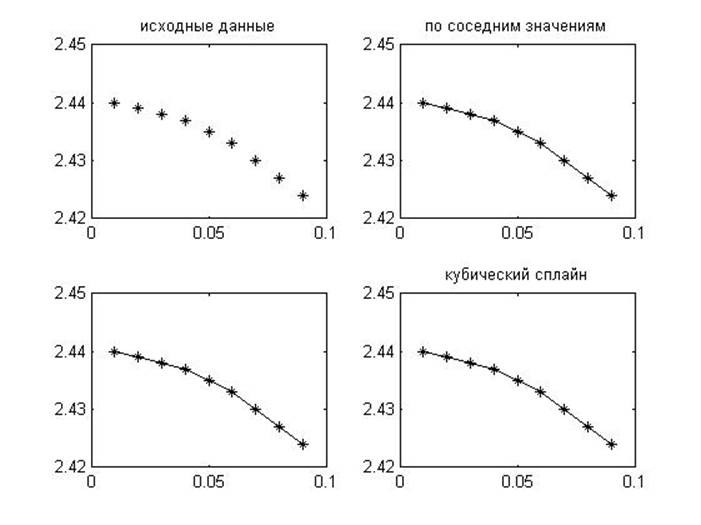
Задание 4
Интерполяция табличных данных
Y=Y+0.08*N
Y =Y +0.96
|
X |
0.010 |
0.020 |
0.030 |
0.040 |
0.050 |
0.060 |
0.070 |
0.080 |
0.090 |
|
Y |
1.480 |
1.479 |
1.478 |
1.477 |
1.475 |
1.473 |
1.470 |
1.467 |
1.464 |
|
Y1 |
2.44 |
2.439 |
2.438 |
2.437 |
2.435 |
2.433 |
2.43 |
2.427 |
2.424 |
>> clf
>> x=[0.010 0.020 0.030 0.040 0.050 0.060 0.070 0.080 0.090]
x =
0.0100 0.0200 0.0300 0.0400 0.0500 0.0600 0.0700 0.0800 0.0900
>> y=[2.440 2.439 2.438 2.437 2.435 2.433 2.430 2.427 2.424]
y =
2.4400 2.4390 2.4380 2.4370 2.4350 2.4330 2.4300 2.4270 2.4240
>> xi=[x(1):0.01:x(length(x))];
>> ynear=interp1(x,y,xi,'nearest');
>> yline=interp1(x,y,xi,'spline');
>> subplot(2,2,1);
>> plot(x,y,'k*');
>> title('исходные данные');
>> subplot(2,2,2);
>> plot(x,y,'k*',xi,ynear,'k-');
>> title('по соседним значениям');
>> subplot(2,2,3);
>> plot(x,y,'k*',xi,yline,'k-');
>> subplot(2,2,4);
>> plot(x,y,'k*',xi,yline,'k-');
>> title('кубический сплайн');
>>
Задание 5
A= zeros(1,20), % аргумент
For i=1:20
А(i)= i*0.1;
End
T=[2.09 ], % выходное значение y
Создание нейронной сети вызов функции new
net=newff([-1 2.09],[5 1]);
{‘tansig’ ‘purelin’};
функция newff создает «классическую многослойную н.с.» с обучением обратного распространения ошибки, т.е изменение весов сенапса, происходит с учетом функции ошибки. Разница между полученными и правильными ответами н.с. распространяется в обратном направлении в примере сеть будет иметь два скрытых слоя.В первом слое 5 нейронов, во втором 1. Функция активации первого слоя tansig, это сигмоидальная функция возвращает выхлдные векторы, в диапозоне от -1 до +1, для второго слоя функция октивации purelin-это ленейная функция активации, возвращает выходные векторы без изменений. В примере задано 50 циклов обучения. Для обучения нейрона сети используется функция train.
net. trainParam.epochs=50
net=train(net,P,T);
y=sim(net,P);
figure(1)
В результате обучения создается график на котором показывается время обучения и ошибка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.