Гипотеза о наличии гетероскедастичности, построение эконометрической модели по методу Эйткена, страница 2

Скопируем значения таблицы Вывод остатка и значения столбца Коэффициенты

	Коэффициенты
Y-пересечение	17,3201628
Переменная X 1	0,094980117
Переменная X 2	-0,000569206

Таким образом эконометрическая модель имеет вид:

3. Исследования наличия гетероскедастичности в массиве исходных данных по непараметрическому тесту Гольдфельда-Квандта

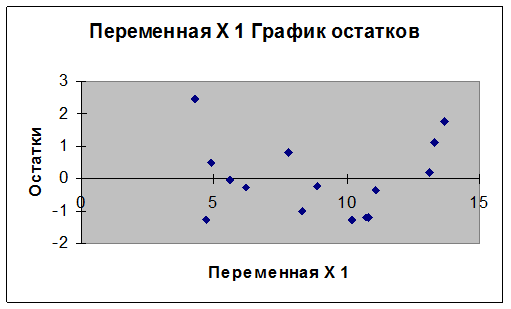
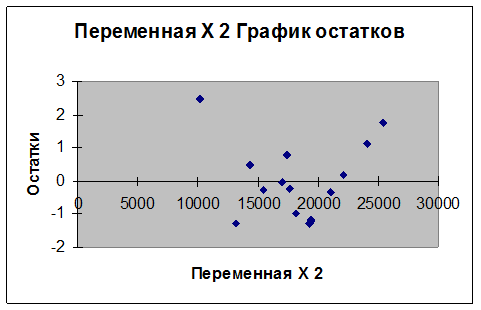
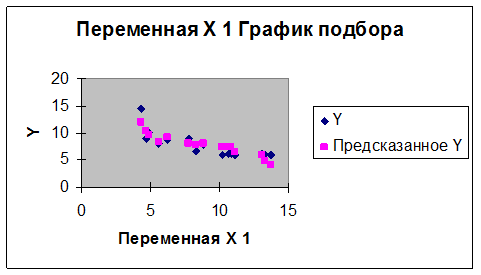
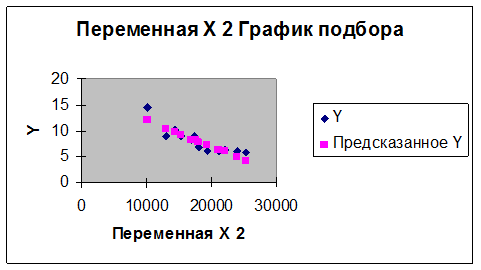
Можно сделать предварительный вывод о гетероскедастичности остатков по графикам остатков х1 и х2 полученных при помощи Регрессии.

Т.к. остатки распределены неодинаково, что видно из графиков то можно утверждать о наличии гетероскедастичности остатков.

Можно проводить исследование на гетероскедастичность по параметрическому тесту Гольдфельда-Квандта.

4. Исследование наличия гетероскедастичности в массиве исходных данных по параметрическому тесту Гольдфельда-Квандта.

Шаг1.  Формулировка нулевой и альтернативной гипотез.

, т.е. гетероскедастичность остатков отсутствует, остатки гомоскедастичны.

Н_А: дисперсия остатков изменяется, существует гетероскедастичность.

Шаг2. Упорядочивание наблюдений по возрастанию фактора

Сортируем по фактору Х1.

Уровень  рентабельности	Затраты оборота
14,4	4,3
9,01	4,7
10,11	4,9
8,13	5,6
8,85	6,2
8,91	7,8
6,78	8,3
7,89	8,9
6,01	10,2
6,1	10,7
6,13	10,8
6	11,1
6,17	13,1
5,98	13,3
5,9	13,7

Шаг3. Отбрасывание С наблюдений, которые содержатся в середине вектора наблюдений.

С=4/15*15=4

Шаг4. построение эконометрических моделей по методу 1МНК для двух полученных совокупностей наблюдений.

Построим 2 эконометрические модели по 2 полученным совокупностям. Условия n1>m+1, n2>m+1, выполняются (6>2, 5>2). Для этого дважды используем регрессию.

Модель 1 Х1

	Коэффициенты
Y-пересечение	15,35919601
Переменная X 1	-0,977467942

Модель 2 Х1

	Коэффициенты
Y-пересечение	6,441911602
Переменная X 1	-0,032734807

Получили 2 эконометрические модели:

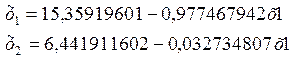
Шаг5. Вычисление статистики F

Таблица 3-Тест Гольдфельда-Квандта