Исчисление средней по сгруппированным данным. Значения коэффициента доверия в таблицах нормального распределения вероятностей

Оглавление

Задача 1. 2

Задача 2. 5

Задача 3. 8

Задача 4. 11

Задача 5. 13

Задача 6. 14

Задача 7. 16

Задача 1.

Методом механического отбора проведено т5-процентное обследование продолжительности разговоров клиентов сотовой компании:

Продолжительность разговора, мин.	Число разговоров
До 2	15
2-4	20
4-6	25
6-8	15
8-10	10
10-12	7
12-14	5
14 и более	3
Итого	100

Определите:

1)  среднюю продолжительность одного разговора (мин.);

2)  с вероятностью Р=0,997 пределы, в которых могут находиться в генеральной совокупности средняя продолжительность одного разговора и доля разговоров более 10 мин.

Решение:

Исчисление средней по сгруппированным  данным  производится  по  формуле средней арифметической взвешенной:

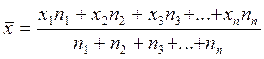
где  х  - отдельные значения признака (варианты)

n – частота повторения признака или вес.

При расчете средней по сгруппированным  данным  в качестве частоты принимается середина интервала.

Продолжительность разговора, мин.	Середина интервала (х)	Число разговоров, (n)	xi∙ni
До 2	1	15	15
2-4	2	20	40
4-6	5	25	125
6-8	7	15	105
8-10	9	10	90
10-12	11	7	77
12-14	13	5	65
14 и более	15	3	45
Итого		100	562

Тогда средняя арифметическая взвешенная будет равна:

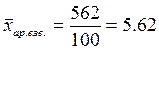минут

Пределы, в которых может находиться в генеральной совокупности средняя продолжительность одного разговора, определим с помощью показателя предельной ошибки выборки.

Предельная ошибка выборки Δ рассчитывается по формуле:

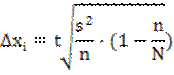
где t – коэффициент доверия, значения которого определяются доверительной вероятностью )

 – выборочная дисперсия;

n-численность выборки;

N –численность генеральной совокупности.

В нашем случае численность генеральной совокупности равна :

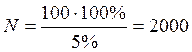 разговоров

Значения коэффициента доверия t задаются в таблицах нормального распределения вероятностей. Чаще всего используются следующие сочетания:

t	P(t)
1	0,683
1,5	0,866
2,0	0,954
2,5	0,988
3,0	0,997
3,5	0,999

В нашем случае при P(t)=0.997   t=3

Найдем выборочную дисперсию:

X	n			n
1	15	-4,62	21,34	320,17
2	20	-3,62	13,10	262,09
5	25	-0,62	0,38	9,61
7	15	1,38	1,90	28,57
9	10	3,38	11,42	114,24
11	7	5,38	28,94	202,61
13	5	7,38	54,46	272,32
15	3	9,38	87,98	263,95
	100			1473,56

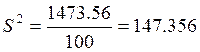
Найдем ошибку выборки:

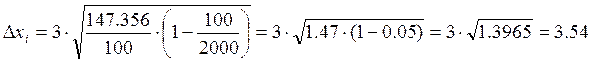
Таким образом, нижний предел будет равен: 5,62-3,54 = 2,08

Верхний предел = 5,62+3,54=9,16

То есть в среднем один разговор длится от 2,08 до 9,16 минут.

Найдем долю разговоров, продолжительностью более 10 минут. Всего таких разговоров (7+5+3) = 15. Доля = 15 /100 * 100% = 15%

Предельная ошибки доли ( при вероятности 0,997) равна:

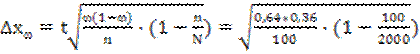
где w – доля разговоров более 10 минут..

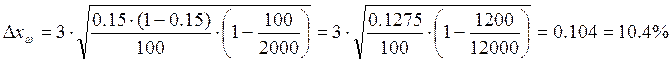
Таким образом пределы доли будут следующими: нижний предел = 15-10,4=4,6%

верхний предел = 15+10,4 = 25,4%

То есть разговоры продолжительностью более 10 минут составляют от 4,6 до 25,4%.

Задача 2.

Имеются следующие данные о стоимости 3-комнатных квартир в двух фирмах по продаже недвижимости (тыс.у.е.):

	Первичный рынок жилья		Вторичный рынок жилья
	фирма 1	фирма 2	фирма 1	фирма 2
1	34	40	25	28
2	37	42	27	30
3	39	47	28	31
4	42	49	30	32
5		51	32	34
6		53	33
7			37

Определите:

1. Общую среднюю стоимость 3-комнатной квартиры на рынке жилья.
2. Среднюю стоимость 3-комнатной квартиры на первичном и вторичном рынке жилья.
3. Общую дисперсию средней стоимость 3-комнатной квартиры.
4. Межгрупповую дисперсию средней стоимости 3-комнатных квартир.
5. Коэффициент эмпирического корреляционного отношения и эмпирический коэффициент детерминации. Сделайте выводы.

Решение:

Найдем средние стоимости квартир как средние арифметические простые:

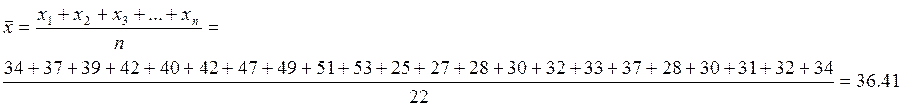
Средняя стоимость квартиры на первичном рынке жилья:

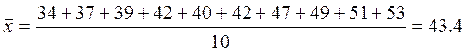
Средняя стоимость квартиры на вторичном рынке жилья:

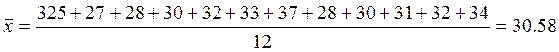
Общая дисперсия  измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Определяется по формуле:

	x
1	34	-2,41	5,80
2	37	0,59	0,35
3	39	2,59	6,71
4	42	5,59	31,26
5	40	3,59	12,89
6	42	5,59	31,26
7	47	10,59	112,17
8	49	12,59	158,53
9	51	14,59	212,89
10	53	16,59	275,26
11	25	-11,41	130,17
12	27	-9,41	88,53
13	28	-8,41	70,71
14	30	-6,41	41,08
15	32	-4,41	19,44
16	33	-3,41	11,62
17	37	0,59	0,35
18	28	-8,41	70,71
19	30	-6,41	41,08
20	31	-5,41	29,26
21	32	-4,41	19,44
22	34	-2,41	5,80
Сумма			1375,32

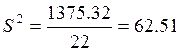
Для определения межгрупповой дисперсии необходимо сначала вычислить внутригрупповую среднюю дисперсию (среднее из дисперсии каждой группы).

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтённых факторов и не зависящую от признака-фактора, положенного в основание группировки.

Найдем внутригрупповую дисперсию по квартирам на  вторичном рынке жилья:

	x
1	34	-9,40	88,36
2	37	-6,40	40,96
3	39	-4,40	19,36
4	42	-1,40	1,96
5	40	-3,40	11,56
6	42	-1,40	1,96
7	47	3,60	12,96
8	49	5,60	31,36
9	51	7,60	57,76
10	53	9,60	92,16
Средняя	43,4
Сумма			358,40

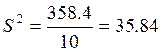
Внутригрупповая дисперсия по квартирам на  первичном рынке жилья:

	x
1	25	-5,58	31,17
2	27	-3,58	12,84
3	28	-2,58	6,67
4	30	-0,58	0,34
5	32	1,42	2,01
6	33	2,42	5,84
7	37	6,42	41,17
8	28	-2,58	6,67
9	30	-0,58	0,34
10	31	0,42	0,17
11	32	1,42	2,01
12	34	3,42	11,67
Средняя	30,58
Сумма			120,92

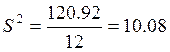
Тогда внутригрупповая средняя дисперсия будет равна: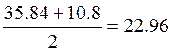

Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки.

Межгрупповая дисперсия: общая дисперсия  - внутригрупповая средняя  =

62.51 – 22.96= 39.55

Эмпирический коэффициент детерминации  – показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии признака и характеризующий силу влияния группировочного признака на образование общей вариации: 39,55 / 62,51 = 0,63

Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации, тогда эмпирическое корреляционное отношение =

Эмпирическое корреляционное отношение может принимать значения от 0 до 1.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:

0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99 Сила связи Слабая Умеренная Заметная Тесная Весьма тесная

Следовательно, связь между показателями тесная.

Вывод: таким образом, средняя стоимость квартир на обоих рынках по двум фирмам составляет 36,41 тыс.у.е., средняя цена квартиры на рынке первичного жилья равна 43,4 тыс.у.е., на вторичном рынка – 30,58 тыс.у.е. В среднем, квадраты отклонений цены от общего среднего значения