Определение количества преподавателей работающих на кафедре высшей математики

Содержание

Задача 1. 3

Задача 2. 3

Задача 3. 3

Задача 4. 6

Задача 5. 6

Задача 6. 8

Задача 7. 9

Задача 8. 9

Задача 9. 9

 

 

Вариант 1

Задача 1

Даны множества: А={1, 7, 9}, B={2, 5, 8, 9}, C={1, 2, 8, 10}, U={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Найти:

а)

б)

в)

=

Задача 9

На кафедре Высшей математики ведётся 3 дисциплины: высшая математика, теория вероятностей, эконометрика. Высшую математику ведут 20 преподавателей, теорию вероятностей – 23. Высшую математику и эконометрику ведут 3 преподавателя. Только теорию вероятностей – 8. только высшую математику – 5, только эконометрику – 2. Все три предмета ведут 3 преподавателя. Сколько всего преподавателей работает на кафедре?

Решение.

Введём обозначения:

А_В – количество преподавателей, ведущих только высшую математику.

А_Т – количество преподавателей, ведущих только теорию вероятности.

А_Э – количество преподавателей, ведущих только эконометрику.

А_ВТ – количество преподавателей, ведущих только высшую математику и теорию вероятности.

А_ВЭ – количество преподавателей, ведущих только высшую математику и эконометрику.

А_ТЭ – количество преподавателей, ведущих только теорию вероятности и эконометрику.

А_ВТЭ – количество преподавателей, ведущих все три предмета.

Отобразим эти множества на диаграмме Эйлера-Вена:

 

Высшую математику ведут 20 преподавателей:

А_В+А_ВТ+А_ВЭ+А_ВТЭ=20                                            (1)

Теорию вероятностей ведут 23:

А_Т+А_ВТ+А_ТЭ+А_ВТЭ=23                                            (2)

Высшую математику и эконометрику ведут 3 преподавателя:

А_ВЭ=3                                                                       (3)

Только теорию вероятностей ведут 8:

А_Т=8                                                                        (4)

Только высшую математику ведут 5:

А_В=5                                                                        (5)

Только эконометрику ведут 2:

А_Э=2                                                                        (6)

Все три предмета ведут 3 преподавателя:

А_ВТЭ=3                                                                     (6)

Подставляя (3), (5) и (6) в (1), получим:

А_В+А_ВТ+А_ВЭ+А_ВТЭ=20

5+А_ВТ+3+3=20

А_ВТ=9

Решая (2), получим:

А_Т+А_ВТ+А_ТЭ+А_ВТЭ=23

8+9+А_ТЭ+3=23

А_ТЭ=3

Тогда общее количество преподавателей:

А=А_Т+А_В+А_Э+А_ВТ+А_ВЭ+А_ТЭ+А_ВТЭ=8+5+2+9+3+3+3=33 преподавателя

Задача 12

Решить систему линейных уравнений методом Крамера:

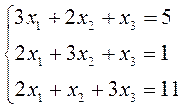
Решение.

Метод Крамера.

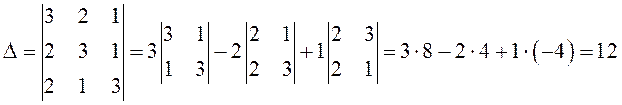
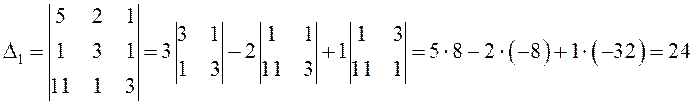
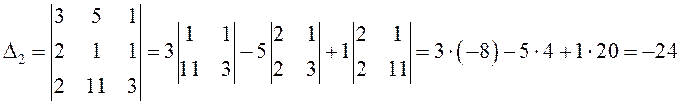
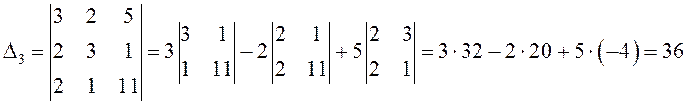
Тогда искомые корни уравнения:

 

Задача 20

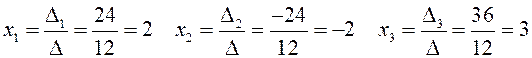
Решить систему линейных уравнений матричным методом:

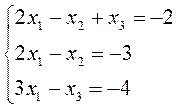
Решение.

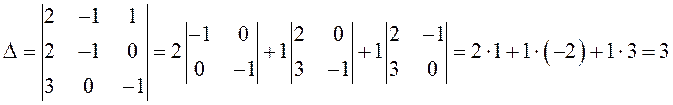
Алгебраические дополнения:

, , ,

, , ,

, ,

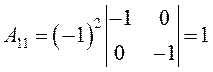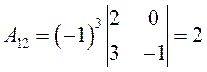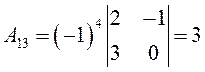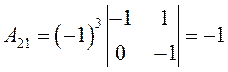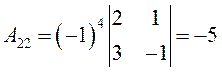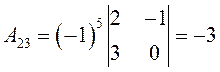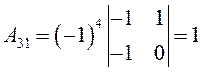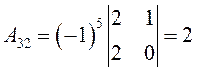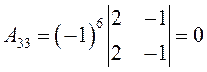
Тогда обратная матрица будет равна:

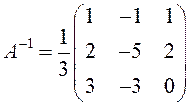
Решение системы в матричной форме:

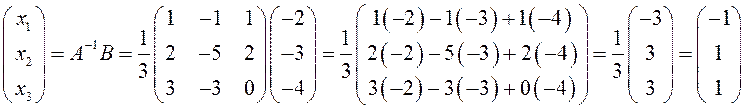
Приравнивая элементы справа и слева, получим:

х₁=–1, х₂=1, х₃=1.

Задача 23

Решить задачу линейного программирования графическим методом

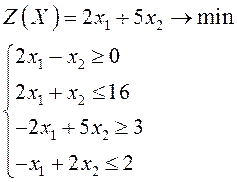
Решение.

В неравенствах системы знаки неравенств заменим на знаки равенств:

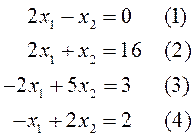
Построим полученные прямые, найдём соответствующие неравенствам полуплоскости и их пересечение.

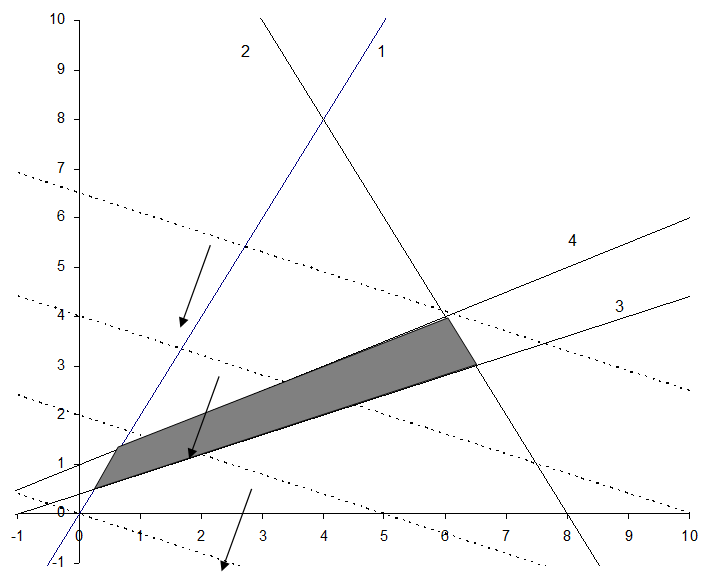
Обратимся к целевой функции . Выразим и построим вектор  и линию уровня, соответствующую значению Z=0 (прямую, проходящую через начало координат перпендикулярно к вектору ). Перемещая линию уровня параллельно самой себе в направлении вектора  до тех пор, пока она будет сохранять общие точки с ОДР, найдём, что в крайнем возможном положении линия уровня пройдёт через точку пересечения прямых 1 и 3. Найдём эту точку:

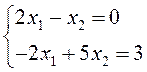
Решим систему:

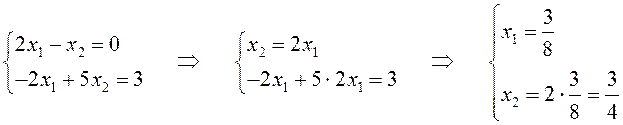
Искомая точка минимума – (х₁, х₂)=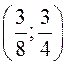. Значение функции в этой точке минимально:

Задача 26

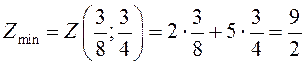
Из букв слова «вероятность» наугад выбирается одна буква. Какова вероятность того, то выбранная буква будет: А – согласной; В – гласной; С – буква «о».

Решение.

В слове «вероятность» всего 11 букв. Из них 4 гласных, 7 согласных букв. Буква «о» встречается два раза.

Искомые вероятности:

Задача 34

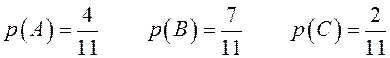
В экзаменационном билете 3 раздела. Из 40 вопросов первого раздела студент знает 30 вопросов, из 30 вопросов второго – 15, из 30 вопросов третьего – 10. Определить вероятность правильного ответа студента по билету.

Решение.

Введём события:

А – студент ответил на вопрос первого раздела.

В – студент ответил на вопрос второго раздела.

С – студент ответил на вопрос третьего раздела.

Вероятности этих событий:

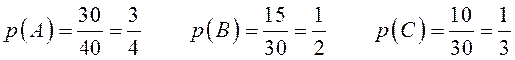
Так как события А, В, С независимы, то вероятность того, что студент ответит на все три вопроса найдём перемножением вероятностей:

Задача 38

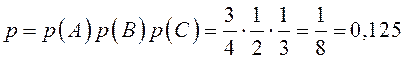
Два автомата производят одинаковые детали, которые поступают на общий контейнер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалось отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Решение.

Введём гипотезы:

Н₁ – деталь произведена 1-ым автоматом, р(Н₁)=2/3.

Н₂ – деталь произведена 1-ым автоматом, р(Н₂)=1/3.

События:

А – деталь, снятая с конвейера, отличного качества

Искомую вероятность найдём по формуле Байеса:

Задача 41

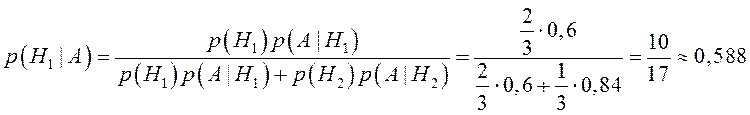
В партии из 25 кожаных курток 5 имеют скрытый дефект. Покупают три куртки. Написать закон распределения вероятностей числа дефектных курток среди купленных. Построить полигон распределения вероятностей. Составить интегральную функцию и построить её график. Найти его числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение.

5 курток из 25 можно отобрать следующим количеством способов:

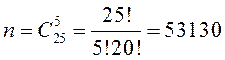
Количество сочетаний, при котором количество дефектных курток 0, 1, 2, 3, 4 или 5:

, ,

, ,

,

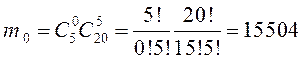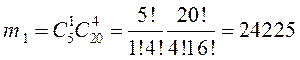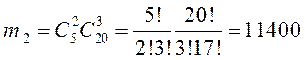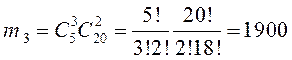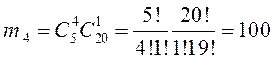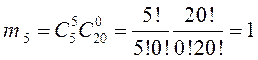
Найдём вероятности, что в партии из 5 курток будет 0, 1, 2, 3, 4 или 5 дефектных курток:

, , ,

, ,

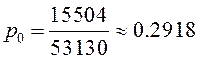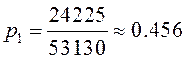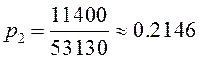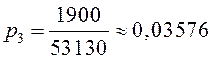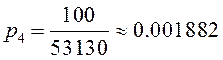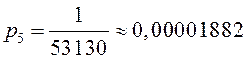
Закон распределения:

х	0	1	2	3	4	5
р	0,2918	0,456	0,2146	0,03576	0,001882	0,00001882

Полигон распределения:

 

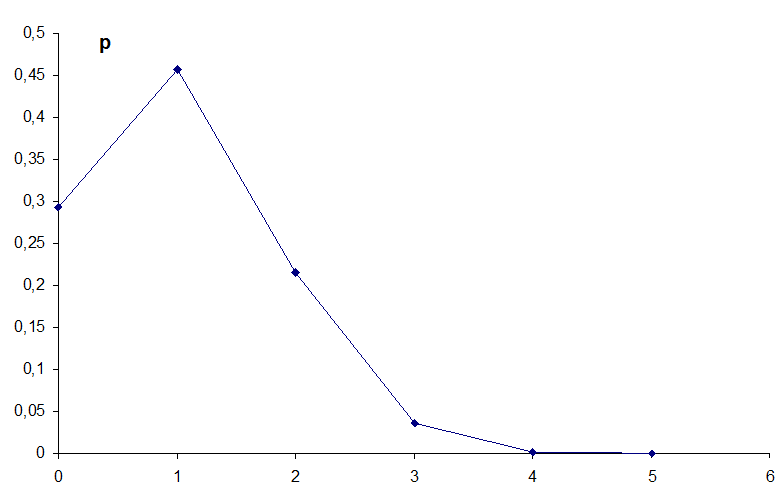
Составим интегральную функцию:

 

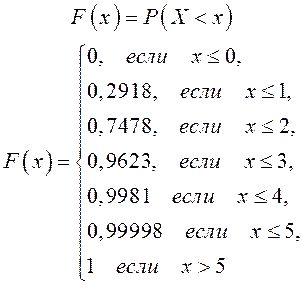
График интегральной функции:

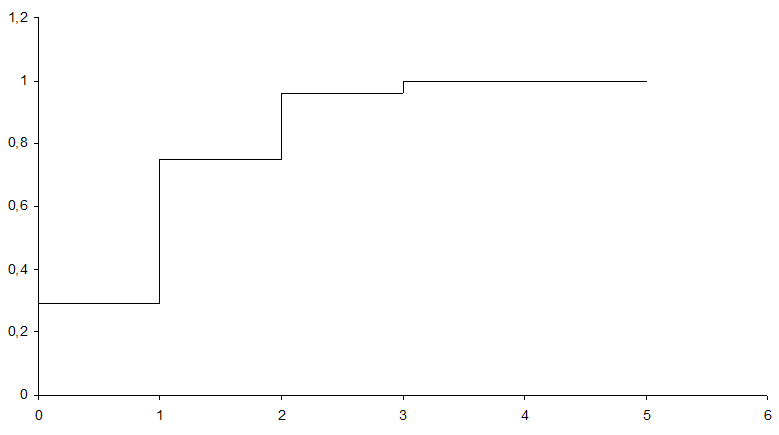
Математическое ожидание:

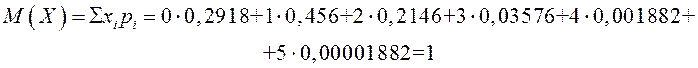
Дисперсия:

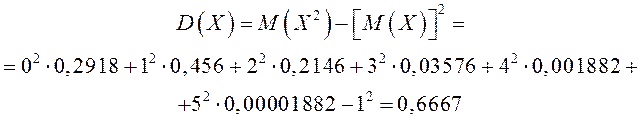
Среднее квадратическое отклонение:

Задача 46

Имеются данные о распределении рабочих по количеству обслуживаемых