Доказать тождество. Номер члена разложения бинома. Средний член разложения бинома

Показатель степени одного бинома на три больше показателя другого. Определить эти показатели, если сумма биномиальных коэффициентов в обоих разложениях вместе равна 144.

4. Найти значение показателя m в разложении бинома   , если коэффициент пятого члена равен коэффициенту девятого члена.

5. В разложении     коэффициенты у четвертого и тринадцатого членов равны между собой. Найти член, не содержащий х.

6. Найти пятый член разложения бинома 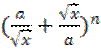  , если отношение коэффициента третьего члена к коэффициенту второго члена равно   .

7. В разложении бинома   коэффициент третьего члена разложения равен 28. Найти средний член разложения бинома.

8. Определить  ,  если пятый член разложения   не зависит от х.

9. Найти наименьшее значение показателя m в разложении  ,  если отношение коэффициентов двух каких-либо соседних членов разложения равно 7:15.

10. Сумма коэффициентов первого, второго и третьего членов разложения равна 46. Найти член, не содержащий х.

11. Найти член, содержащий в разложении бинома  .

12. Найти тринадцатый член разложения   , если биномиальный коэффициент третьего члена разложения равен 105.

13. При каком значении n коэффициенты второго, третьего и четвертого членов разложения бинома   составляют арифметическую прогрессию?

14. Найти, при каких значениях х в разложении бинома   сумма третьего и пятого членов равна 135, если сумма биномиальных коэффициентов трех последних членов равна 22.

15. Определить, при каком значении х шестой член разложения бинома   равен 21, если известно, что биномиальные коэффициенты второго, третьего и четвертого членов разложения представляют соответственно первый, третий и пятый члены арифметической прогрессии.

16. В разложении бинома 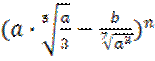  определить член, содержащий а в третьей степени, если сумма биномиальных коэффициентов, стоящих на нечетных местах в разложении бинома, равна 2048.

17. В разложении бинома 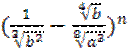  определить член, содержащий , если отношение биномиальных коэффициентов четвертого и второго членов равно 187.

18. В разложении бинома 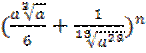    определить член разложения, не содержащий а, если сумма биномиальных коэффициентов трех первых членов разложения равна 79.

19. В разложении бинома     определить член, не содержащий х, если сумма биномиальных коэффициентов второго члена от начала и третьего от конца разложения равна 78.

20. Определить х, если четвертый член разложения бинома 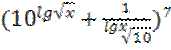  равен 3500000.

21. Коэффициенты пятого, шестого и седьмого членов разложения бинома   составляют арифметическую прогрессию. Найти n.

22. Шестой член разложения бинома   равен 5600. Найти х.

23. Отношение коэффициента третьего члена к коэффициенту пятого члена разложения бинома     равно 2/7. Найти тот член разложения, который содержит .

24. В разложении бинома   сумма коэффициентов на 240 меньше суммы коэффициентов разложения бинома  . Найти третий член первого разложения.

25. Определить, при каком значении х разность между увеличенным в 9 раз третьим членом разложения бинома 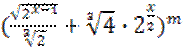  и пятым членом того же разложеня равна 240, если известно, что разность между логарифмом утроенного биномиального коэффициента четвертого члена разложения и логарифмом биномиального коэффициента втого члена равна 1 (логарифм по основанию 10).

Задание №3.

1. В классе изучается 10 предметов. В среду шесть уроков, при этом все уроки различны. Сколькими способами можно составить расписание на среду?

2. Сколько различных четных пятизначных чисел с неповторяющимися цифрами можно составить из цифр 0, 1, 3, 4, 5?

3. Сколькими способами можно выбрать из 15 человек партию людей для работы, если в нее может входить любое число людей от одного до пятнадцати?

4. Сколько можно составить четырехзначных чисел из пяти различных цифр 0, 1, 2, 3, 4, если цифры в числе не повторяются?

5. На рояле 88 клавиш. Сколько существует последовательностей из шести попарно различных звуков (в последовательности звуки идут один за другим)? Сколько существует аккордов из шести звуков (аккорд получается, если любые 6 клавиш нажаты одновременно)?

6. Компания из семи юношей и десяти девушек танцуют. Если в каком-то танце участвуют все юноши, то сколько существует вариантов участия девушек в этом танце? Решить этот же вопрос, если относительно двух девушек можно с уверенностью сказать, что они будут приглашены на танец.

7. Имеется шесть пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были различных размеров?

8. Сколько размещений из m элементов по n будет начинаться любым элементом за исключением первого?

9. Каждого из семи студентов можно направить для прохождения практики в одну из двух школ. Сколькими различными способами это можно сделать?

10. Сколько всех делителей у числа 30030?

11. Сколько четных четырехзначных чисел можно изобразить цифрами