Циклические и сверточные коды. Принципы формирования циклических кодов. Алгоритм формирования циклического кода

Занятие № 7. “Циклические и сверточные коды”

1. Принципы формирования циклических кодов

Циклические коды получили широкое распространение благодаря их эффективности при обнаружении и исправлении ошибок. Эти коды получили такое название потому, что основной операцией кодирования является циклическая перестановка.Сущность циклической перестановки заключается в том, что последний символ кодовой комбинации занимает место первого, первый – второго, и т.д.

Если циклической перестановке подвергалась разрешенная кодовая комбинация, то в результате этой операции появляется новая разрешенная комбинация, что является основным свойством циклических кодов.

Для построения циклические коды достаточно знать порождающую матрицу. Но можно указать и другой способ построения циклических кодов, базирующийся на использовании неприводимых многочленов, в этом случае процесс кодирования сводится к отысканию многочлена (из известных неприводимых многочленов) соответствующего информационной последовательности.

Неприводимым называется многочлен, который не может быть представлен в виде произведения многочленов низших степеней, т. е. такой многочлен делится только на самого себя или на единицу и не делится ни на какой другой многочлен. На такой многочлен делится без остатка двучлен .

Над многочленами можно производить все алгебраические действия.

При этом сложение двоичных многочленов сводится к сложению по модулю два коэффициентов при равных степенях переменной .

Умножение производится по обычному правилу перемножения степенных функций, однако полученные в этом случае коэффициенты при данной степени складываются по мо дулю два.

Деление осуществляется по правилам деления степенных функций, при этом операции вычитания заменяются операциями суммирования по модулю два.

При рассмотрении циклического кода, можно представить комбинацию двоичного кода не в виде последовательностей нулей и единиц, а в виде полинома некоторой степени:

В этом случае циклическая перестановка есть результат умножения данного полинома на :

Однако в последнем члене необходимо заменить  на 1 (в противном случае длина кодовой комбинации превысит ).

Учитывая, замену  на 1 в произведении  получаем новый полином, коэффициенты которого образуют новую разрешенную комбинацию:

Полином  степени , на который делится без остатка двучлен , называют порождающим полиномом циклического кода.

Проверочный полином, образуется как результат деления двучлена на порождающий полином: .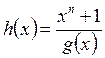

Произведение , поэтому полиномы  и  рассматривают как ортогональные и данная операция лежит в основе построения алгоритмов декодирования.

Рассмотрим как строится циклический код (7,4) взяв в качестве порождающего полинома .

Докажем, что выбранный полином является порождающим, для этого произведем деление двучлена на выбранный полином:

т.к. результат деления получили без остатка, то  действительно порождающий полином.

Полученный полином  является проверочным.

Принцип обнаружения ошибок при помощи циклического кода заключается в том, что в качестве разрешенных принимаются только те комбинации, которые без остатка делятся на заранее выбранный образующий многочлен g(x). Если принимаемая комбинация искажена, то это условие на приемной стороне не будет выполнено. В результате этого формируется сигнал, указывающий на наличие ошибки.

Задача кодирования состоит в том, чтобы сформировать кодовые комбинации на передаче, удовлетворяющие указанному условию.

Метод построения кодовых комбинаций.

В процессе кодирования кодовая комбинация (С) отображающая двоичный код передаваемого сообщения (примитивный код) умножаются на х^r. При этом длина кодовой комбинации увеличивается на r разрядов. Эти дополнительные разряды будут проверочными. Полученное произведение C×x^r делят на специально подобранный образующий многочлен g(x). При этом получают остаток R. Данный остаток R суммируют с произведением C×x^r. Получают кодовую комбинацию C”= C×x^r +R, которая будет без остатка