Векторно-матричный умножитель – простейший оптический процессор.
Краткая аннотация работы:
Операция умножения вектора на матрицу широко используется как в рамках традиционных вычислительных процедур, так и в таких новых направлениях, как нейрокомпьютинг, искусственные нейронные сети и, шире, в рамках парадигмы вычислительного интеллекта. Широкое применение этой математической операции в фундаментальной проблеме искусственного интеллекта обусловлено прежде всего тем, что простые операции произведения векторов и умножения вектора на матрицу позволяют реализовать различные модели ассоциативной памяти. Напомним, что именно ассоциативная память суть основа любой системы искусственного интеллекта, так как без памяти нет и интеллекта.
Задачи, решаемые в работе:
1. Численное моделирование
1.1. обучения сети (вычисление матрицы весовых коэффициентов (связей) для заданных пар векторов);
1.2. выходного вектора
2. Экспериментальное исследование выходного вектора при предъявлении обученной сети разных векторов.
Сведения из теории:
Векторно-матричный формализм широко применяется для описания состояния и поведения искусственных нейронных сетей. В рамках этого подхода состояния нейронных слоев описываются посредством векторов-строк, размерность такого вектора равна количеству нейронов в слое, состояние (уровень активации или возбуждения) каждого нейрона определяет значение соответствующего компонента вектора. Напомним, что в простейшем случае нейроны, объединенные в один слой, не связаны друг с другом, межнейронные связи реализуются только между нейронными слоями. Простой и удобный метод формирования матрицы связей между двумя слоями нейронной сети, например, слоями A и B, дает модель векторного произведения W=ATB, где T – символ транспонирования. Размерность матрицы связей W m´n, где количество строк m – число нейронов слоя A, а количество столбцов n – число нейронов слоя B. Например, wi,j – это вес, связывающий i-ый нейрон ai с j-ым нейроном bj. Нетрудно видеть, что этот метод может рассматриваться как реализация правила обучения Хэбба, подробно рассмотренного в лекционном курсе.
Такая модель позволяет реализовать идею ассоциативной памяти, понимаемой как восстановление эталона при предъявлении его искаженной или фрагментированной версии (авто-ассоциативная память) или сопряженного с эталоном вектора (гетеро-ассоциативная память). Действительно, предъявление обученной сети с матрицей W эталонного вектора A описывается как умножение вектора на матрицу AW=AATB=B, т.е., поскольку AAT суть скаляр, то в слое B восстанавливается эталонный вектор B. Если предъявляется вектор A’, отличный от эталонного A, то A’W=A’ATB=B’, то, поскольку величина A’AT меньше, чем AAT, в слое B восстанавливается вектор B’, который можно трактовать как «ослабленный» вектор B (B’=A’ATB<AATB=B).
Если матрица связей W представляет собой сумму матриц, каждая из которых сформирована своей парой векторов Wk= AkBk, то при предъявлении такой вектора A’ в слое B восстановится сумма A’A1TB1 + A’A2TB2 +…+ A’AkTиk ; наибольшую величину произведения A’AkT и, соответственно, наибольшую интенсивность восстановленного вектора Bk даст та матрица Wk, для которой входной вектор A’ наиболее похож на эталонный вектор AkT , остальные восстановленные вектора B будут слабее, чем Bk.
Аналогичная процедура возможна и при распространении информации от слоя B к слою A через транспонированную матрицу WT. Если процедура прохождения информации от слоя A к слою B и обратно повторяется многократно, и нейроны обладают нелинейной активационной функцией, то в результате сеть сойдется к устойчивому состоянию - в обоих слоях восстанавливаются эталонные вектора Ak и Bk, «очищенные» от остальных пар векторов Aи B. Такая модель известна как двунаправленная ассоциативная память, предложенная Бартом Коско.
Операция умножения вектора на матрицу требует достаточно больших вычислительных ресурсов. В то же время, оптика позволяет реализовать эту операцию «в параллель» в реальном времени – сама операция реализуется со скоростью света, основные затраты времени необходимы для ввода информации в процессор и считывания результата. Оптика позволяет реализовать операции произведения двух векторов-строк – в этом случае матрица может быть реализована как плоский транспарант или тонкая голограмма, пропускание каждой ячейки которого (дифракционная эффективность элементарной тонкой голограммы) пропорциональна или равна результату произведения соответствующих компонент, а также умножение вектора на матрицу. Матрица связей вектора-строки с 2-D матрицей будет иметь размерность 3-D и может быть реализована при использовании объемных регистрирующих сред. Матрица связей двух 2-D матриц будет иметь размерность 4-D и технические методы реализации таких матриц в нашем трехмерном мире пока не известны. (Известны методы использования пространственного, временного, частотного и др. разнесения, но, строго говоря, они представляют собой «обходные пути».)
В данной работе студентам надлежит исследовать операцию умножения вектора-строки на матрицу.
Экспериментальная установка (принципиальная оптическая схема эксперимента):
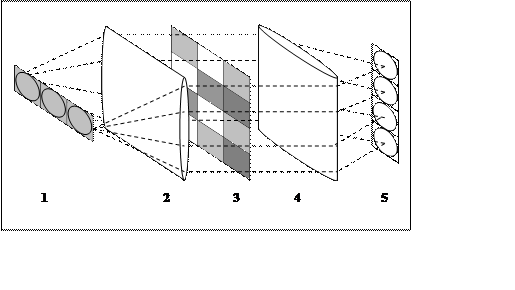
Рис.1. Принципиальная схема векторно-матричного умножителя.
1- линейка излучающих светодиодов (3 шт.), 2 и 4 – цилиндрические линзы, 3 – матрица транспарантов 3×4, 5 – линейка фотоприемников (фотодиодов) (4 шт.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.