1-11. Разложение сложного сигнала по системе базисных функций. Определение базисных функций, выбор системы базисных функций в ИТ. (в сканере конспекта стр. 15-16)
Спектральная (частотная) форма представления сигналов использует разложение сигнальных функций на гармонические составляющие. Разложение сложного сигнала по системе базисных функций – это один из способов спектрального представления сигнала. (остальные – прямоугольная волна, вейвлет базис ), суть которого заключается в представлении сигнала в виде суммы элементарных сигналов.
X(t) = CiFi(t)
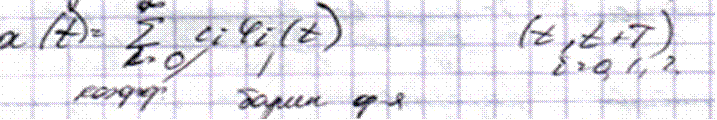
Базисная функция – это функция, удовлетворяющая следующие условия:
Технологические требования:
1-12. Примеры систем базисных функций и соответствующих спектральных представлений сигналов. Системы тригонометрических функций, комплексных экспоненциальных функций, функций Хаара. Вейвлет-базис. Их применение в ИТ.
Система тригонометрических функций.
Применение: (гармонические сигналы) – приемники резонансного типа, камертон
Гармонический спектроанализатор.
Амплитудный и фазовый (спектры сигнала)
Только по амплитудному спектру нельзя восстановить сигнал.
Расширением гармонического спектра является комплексно-экспоненциальный спектр.
При бесконечном росте периода Т, частоты сближаются, образую непрерывный базис, и сумма переходит в интеграл Фурье. Т.о. непериодический сигнал раскладывается не в ряд Фурье, а в интеграл Фурье. У случайного сигнала раскладывается не амплитуда, а корреляционная функция => у случайного сигнала отсутствует базовый спектр.
Вейвлеты (короткие волны) – это функции определенной формы, локализованные по оси независимых переменных, инвариантные к сдвигу и линейные к операции масштабирования (сжатия/растяжения). Они создаются с помощью специальных базисных функций, которые определяют их свойства. По локализации во временном и частотном представлении вейвлеты занимают промежуточное положение между гармоническими функциями, локализованными по частоте, и функцией Дирака, локализованной во времени. Теория вейвлетов не является фундаментальной физической теорией, но она дает удобный инструмент для решения многих практических задач. Основная область применения вейвлетных преобразований – анализ и обработка сигналов и функций, нестационарных во времени или неоднородных в пространстве, когда результаты анализа должны содержать не только общую частотную характеристику сигнала (распределение энергии сигнала по частотным составляющим), но и сведения об определенных локальных координатах, на которых себя проявляют те или иные группы частотных составляющих, или на которых происходят быстрые изменения частотных составляющих сигнала. По сравнению с разложением сигналов на ряды Фурье, вейвлеты способны с гораздо более высокой точностью представлять локальные особенности сигналов, вплоть до разрывов 1-го рода (скачков). В отличие от преобразований Фурье, вейвлет-преобразование одномерных сигналов обеспечивает двумерную развертку, при этом частота и координата рассматриваются как независимые переменные, что дает возможность анализа сигналов сразу в двух пространствах.
Вейвлет-базис.
Вейвлет анализ - Обобщение спектрального анализа.
В отличие от традиционного преобразования Фурье, вейвлет преобразование – это 2-мерное представление сигнала в плоскости. Частота – положение. Аналог частоты – 1/a, а положение характеризуется сдвигом.
Возможны различные базисные функции для вейвлет преобразований.
Требования к базисной функции
Кроме первого момента существует вейвлет внешних порядков. Они подавляют медленно состояние сигнала и обеспечивают анализ тонкой структуры сигнала.
Первый шаг 2мерного вейвлет преобразования – выделение одной низкочастотной и 3 высокочастотных компоненты исходного изображения.
Применение вейвлет преобразования.
Сжатие изображения (из высокочастотных компонентов выбрасываются
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.