Интерференция последствий выбора в результате одновременного выбора альтернатив. Обобщенное дерево вероятностей. Необходимость разработки системной (эмерджентной) теории информации

получает смысл единиц, в которых измеряется неопределённость (и соответственно количество информации при её устранении), например, бит для двоичных логарифмов или нат для натуральных. В литературе, в том числе и серьёзных авторов, распространена ошибка, когда информацией сичтается только то, что выражено в двоичной системе исчисления и соответственно в битах. Это именно и только ошибка!.

Ещё одно напоминание. Энтропия – аддитивная переменная. Поэтому нуль отсчёта для неё может быть задан произвольно. В теории информации для средств связи это отражает факт, что информация подразумевается относящейся к чему-то конкретному, то есть говорят «информация о том-то». 

В связи со знаками для энтропии как характеристике неопределённости и информацией как устранённой неопределённостью необходимо ещё одно пояснение. Казалось бы, информацию нужно понимать в связи с этим как энтропию с отрицательным знаком. Однако в теории информации для средств связи такого изменения знака нет – сама энтропия есть одновремено и мера неопределённости, и мера информации. Потому и в природе нет необходимости приписывать информации смысл отрицательной энтропии. Термин негэнтропия Л. Бриллюэна здесь не обсуждаю, так как в его основе лежит существенная некорректность Бриллюэна. 

Участие вероятностей в осуществлении событий, рассматриваемых в теории связи, выражается тем, что устранение неопределённости есть увеличение вероятности наступления того, что задано как цель. Поэтому вероятности должны участвовать в математической формулировке величины устранённой неопределённости, то есть в определении информации. Формулы с участием логарифма будут описывать энтропию и при предпосылках более узких, чем приведены выше. Их конкретный вид получит соответствующие подробности. 

Первая удачная попытка реализовать определение информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в данных условиях  n  вариантов некоторого результата. Целью является один из них. Хартли предложил характеризовать неопределённость логарифмом числа  n.  То есть  log n  является количественной мерой неопределённости. Выбор основания логарифма связан с понятием об алфавитах для описания информации. Этот выбор существенен для экономичности кодирования в технических устройствах или живых системах (сокращения потоков импульсов или аналоговых сигналов), но, как напоминалось выше, не меняет самого количества информации как устранённой неопределённости за счёт того, что перед логарифмом вводится безразмерный множитель, выражаемый модулем перехода между основаниями логарифмов. От него зависят названия единиц информации.

При математическом описании неопределённости (например способом Хартли) в случае равновероятных результатов можно перейти от их числа  n  к обратной величине – вероятности  р  одного из них. В терминах связи конкретно говорят о вероятности переданного сообщения   р₀   у приёмника до приёма сообщения. Устранение неопределённости выражается тем, что вероятность переданного сообщения у приёмника после приёма сигнала возрастает и становится   р₁ .  Тогда количественная мера  s  полученной информации (устранённой неопределённости) выражается логарифмом отношения вероятностей:

.

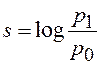Оно равноправно по отношению к любому конкретному сообщению и имеет разную величину в зависимости от величин   р₀  и   р₁   для него. В частном случае, когда при передаче полностью отсутствую шумы и сбои, искажающие сигнал, вероятность  р₀  равна единице.

Недостаток этого определения в том, что оно справедливо в приближении равновероятности всех исходов. Это выполняется далеко не всегда. В пределе в этом определении невероятному исходу приравнивается неизбежный. В 1948 г. это исправил К. Шеннон, который определил в качестве меры неопределённости конкретное выражение:

, где 

есть вероятности отдельных исходов. Он предложил называть эту величину “энтропией”, не поясняя связей и различий этого термина с общеизвестой энтропией в физике. Происхождение знака минус в предыдущей формуле то же самое, что пояснялось выше. Определение Шеннона сокращённо зависывают в виде:

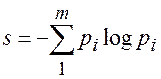, подразумевая как очевидное, что признаки (аргументы), по отношению к которым определены события и их вероятности, могут быть существенно разными, а эта формула (суммирование в ней) справедлива только для однородных признаков.

Опуская подробности, надо напомнить, что конкретный вид этой формулы