Методы спектрального разложения сигналов. Понятие спектрального разложения сигнала. Разложение сигнала по ортогональным полиномам

Необходимость использования нетригонометрических базисов при разработке аппаратуры спектрального анализа обусловлена расширением круга применения средств цифровой и импульсной техники, микросхемотехники и цифровой обработки на основе больших интегральных схем.

В основе аппаратурного спектрального анализа по нетригонометрическим базисам лежит структурная схема, приведенная на рис. 1.4. Генератор базисных функций предназначен для формирования ортогональных колебаний  ϕ_k, вид которых  определяется на основе априорных данных об анализируемом сигнале. Анализатор спектра обычно представляет собой

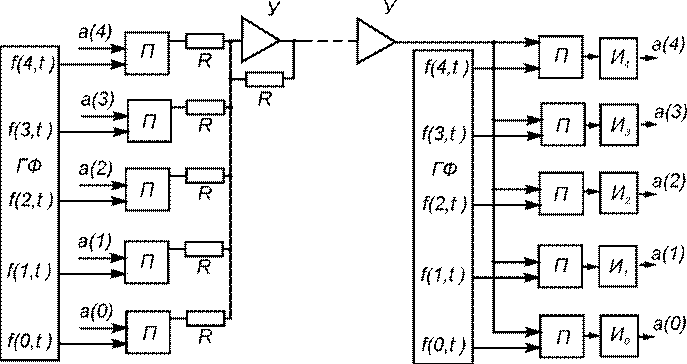
Рисунок 1.5. Функциональная схема системы передачи пяти коэффициентов a_i с использованием ортогонального разделения

параллельную схему, состоящую из  N каналов, каждый из которых состоит из устройства умножения (УУ) и устройства суммирования (УС). На первые входы УУ через входное устройство (ВУ) поступает анализируемый сигнал x(t), а на вторые  базисные функции . Результаты перемножения в соответствии с прямым преобразованием Фурье  накапливаются в УС в течение интервала наблюдения. Получаемые при этом величины на выходах УС численно равны коэффициентам разложения a_k (k = 0, 1, , N-

1).  

Применение негармонических ортогональных базисов не ограничивается лишь задачами анализа спектра. На рис. 1.5 показана функциональная схема системы для передачи пяти коэффициентов a несколькими ортогональными функциями. На передающем конце генератор функций ГФ генерирует пять сигналов f (0,t), , f (4,t), которые ортогональны на интервале 0≤t<T. Пять коэффициентов a(0), , a(4) представлены в виде уровней напряжений, имеющих постоянное значение в течение интервала времени 0≤t<T. В перемножителях П базовые функции f(i,t) умножаются на коэффициенты a(i). Пять произведений a(i) f(i,t) суммируются с помощью резисторов R и операционного усилителя У. Полученный сигнал передается по линии связи. На приемной стороне принятый сигнал поступает через усилитель У на пять перемножителей, где одновременно перемножается с каждой из пяти функций f (i,t), используемых в передатчике в качестве переносчиков коэффициентов. Генераторы функций ГФ в передатчике и приемнике должны быть синхронизированы. Сигналы, полученные на выходах перемножителей, интегрируются в интеграторах в течение интервала времени  0≤t<T.

Выходные напряжения интеграторов в момент времени t = T представляют собой коэффициенты a(0), , a(4). Другой набор из коэффициентов a(0), , a(4) передается в течение интервала времени T. Таким образом, базисные функции являются периодическими с периодом T. Напряжения, соответствующие в передатчике коэффициентам a(i) на интервале времени 0≤t<T, мгновенно меняются в момент времени t = T и остаются в соответствии с коэффициентами a(i) на интервале T≤t<2T. Интеграторы в приемнике в момент времени t = T возвращаются в исходное состояние и начинают интегрировать напряжения, поступающие от перемножителей на интервале времени T≤t<2T.

Для практического применения функциональная схема, изображенная на рис. 1.5, должна быть дополнена цепью синхронизации. 

1.5.3. Методы фурье-оптики

Говоря об аппаратурных методах  выполнения гармонического анализа, нельзя не упомянуть оптические методы получения спектра одномерных  и двумерных пространственных и временных сигналов, обладающие рядом уникальных свойств. В основе  этих методов, называемых фурье-оптикой [20], лежит свойство линзы выполнять преобразование Фурье функции пропускания объекта, на котором происходит дифракция. Структурная схема когерентно-оптического спектроанализатора  показана на рис. 1.6. Измеряемый объект (транспарант) расположен перед линзой в кювете с иммерсионной жидкостью, что позволяет устранить в нем нежелательные фазовые неоднородности. При таком расположении транспаранта (непосредственно вблизи линзы) в фокальной плоскости линзы формируется двумерный фурье-спектр транспаранта. Особенность такой системы состоит в том, что процессор, построенный на основе такой системы выполняет преобразование со скоростью света, независимо от того, обрабатывается ли 100 или 10⁶ элементов изображения. При этом возможно достижение достаточно высокого разрешения. 

Практические реализации систем на основе фурье-оптики являются