Goodness(d, С) =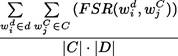 
После того, как мы оценили документ с точки зрения всех коллекций мы можем выбрать одну или несколько наиболее высоких оценок и классифицировать документ в одну или несколько коллекций.
Вычисления тематической близости пары термов представляет собой вычисление вероятности использования этой пары термов в документах одной тематики. Эта вероятность оценивается по результатам анализа использования термов в множестве документов, которыми описываются тематики.
Один из возможных вариантов оценки этой вероятности состоит в следующем. По набору документов строится матрица термы-на-Дтсументы Х, строки которой отражают распределение термов по документам. В качестве оценки тематической близости двух термов используется скалярное произведение соответствующих строк этой матрицы. Таким образом для вычисления оценок близости между всеми парами термов достаточно вычисјшть матрицу ХХ
Такой подход аналогичен классическим методам поиска информации основанных на векторном представлени:и описания документа. Поэтому ему присущи те же недостатки:
е метод не обнаруживает зависимости между термами, которые часто используются в документах одной и той же тематики, но редко встречаются вместе
• случайные зависимости и ошибки правописания оказывают существенное влияние на получаемые оценки и негативно сказываются на точности метода
• размер матрицы термы-на-Дтсументы очень велик даже для небольшого (с точки зрения статистики) числа документов и поэтому использование этой матрицы весьма ресурсоемко
Дальнейшим развитием такого подхода является использование латентно-семантического анализа.
По матрице ХХ т строится ее
аппроксимация ХХ Т 
где Х — это аппроксимация Х полученная методом
латентно-семантического анализа на базе разложения по сингулярным значениям
(подробности в разделе 2). Таким образом:
Ях т = 
ХХТ
= 
и в силу ортонормированности матрицы Vlsa
Отметим, что диагональная матрица Е имеет размерность К, где К — это выбранная при аппроксимации желаемая размерность пространства гипотез. Таким образом при таком подходе трудоемкость вычисления тематической близости двух термов при вычисленных матрицах Ulsa и Elsa составляет О(К), т.е. она не зависит от количества анализируемых документов и размера общего словаря.
Функция тематической близости двух термов FSR(t01 , и») однозначно задается матрицей ХХ т •
FSR(U1,
и») = 
и]
Для практической проверки эффективности описываемого метода мы провели ряд экспериментов, используя большой стандартный набор данных в качестве экспериментальной базы.
В качестве основной экспериментальной базы мы воспользовались набором данных, предоставляемых Text REtrieval Conference (TREC) [11]. Эти наборы являются наиболее известными стандартными наборами тестовых данных в области поиска информации (information retrieval).
.1 2 з 4 5
Number rof collections
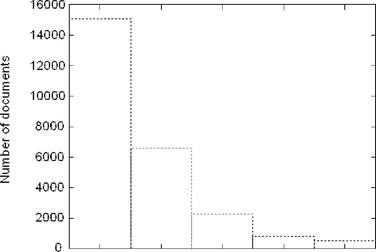
Рис. 1: Распределение документов по количеству соответствующих им тематик
lntersectian
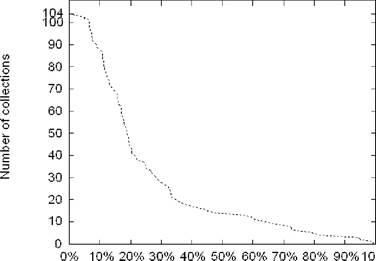
Рис. 2: Процент максимального пересечения тематик
В рамках этой работы мы использовали подмножество документов из коллекции Los-Angeles Times с диска TREC-5. Коллекции TREC не разбиты явным образом на тематические группы, но для каждого документа из коллекции Los-A ngeles Times экспертами указано одна или несколько тем к которым этот документ относится. Среди всех встречающихся тем мы отобрали те, которые упоминаются в не менее чем 200 документам. Таким образом мы получили 104 тематические группы. Более подробная информация об используемом наборе тестовых данных представлена в таблице 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.