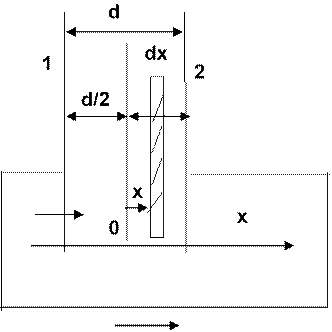
Наведение тока в плоском зазоре при прохождении промодулированного по плотности электронного потока

Наведениетока в плоском зазоре при прохождении промодулированногопо плотности электронного потока.

ρ= ρ ρ ω₀ + ₁sin t

где ρ₀- постоянная составляющая, ρ₁- амплитуда переменной составляющей iконв = ρSv0 = I0 + Im sinωt

где I = _m ρ₁Sv , I = _{0 0} ρ₀Sv , S - ₀ площадь сечения тока когда E=0:

dx

dq = iконвdt = iконв

v0

v₀     dx      x diнавед = dq d = iконв d          t = t0 + v0

ωt          i

d                                                                           sin          навед

         i       = 2∫ ⎧⎪⎨I0 + Im sin⎛⎜^⎜ωt + ₂ω_vt ⎟⎟⎞⎬⎫⎪ dx_d = I0 + Im sinωt0 _ω2_tv₀

навед

_{−d ⎪⎩               ⎝           0 ⎠⎪⎭}

2                                                                             2v

0

θ θ

Введем параметр: γ = sin

22

iнавед = I0 +γIm sinωt0

Наведенныйток при модуляции потока электронов

ωt

d                                                                                 sin

iнавед = 2∫ ⎪⎨⎧I0 + Im sin⎛⎜_⎜ωt + ₂ω_vt _⎟⎟⎞⎬⎫⎪ dx_d = I0 + Im s ni ωt0 _ω2_tv₀

_{−d ⎪⎩                ⎝            0 ⎠⎪⎭}

2                                                                                    2v

0

ωd d      sin

iнавед = 2∫ ⎧⎪⎨I0 + Im sin⎛⎜⎜ωt0 +ωx ⎞⎟⎟⎫⎪⎬ dx 0 2v0 = I + Im sinωt

−d ⎪⎩                ⎝          v0 ⎠⎪⎭ d                               0 ωd

2                                                                                    2v

0

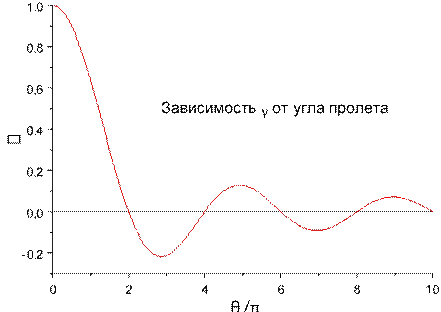
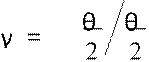sin , коэффициент взаимодействия электронного потока с электрическим полем iнавед = I0 +γIm sin ωt0

Методыуправления электронными потоками на СВЧ

z  Электростатическое управление

z  Управление с помощью сетки с отрицательным потенциалом, создающей модуляцию конвекционного тока

z  Динамическое управление z Управление, полезно использующее конечное время пролета электронов

iконв = I0 + i(t),

Методыуправления электронными потоками на СВЧ

Периодическое изменение скорости электронов, производимое в специальном управляющем устройстве (например, в резонаторе или замедляющей системе), получило название модуляции электронного потока по скорости.

Модуляцияв резонаторе

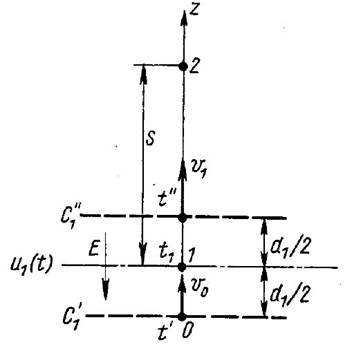U =U_m sin(ωt)

Энергия электрона при прохождении зазора dx:

dW = eUm sinωtdx

d

Полное приращение энергии: d

                                                     θ

  ∆W = −2d eUd^m sin(ωt0+^ωv0^x)dx eU= m sinωt0sin^[1] =e Uγ m sinωt0

∫

0

Модуляцияв резонаторе

Полная кинетическая энергия электрона:

2

mv

= eU + e Uγ sinωt

2  0   _m     0 отсюда:

V =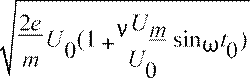

U^m

Полагая U_m U₀ разложим V в ряд по переменной =ξ . U0 Получим:

v 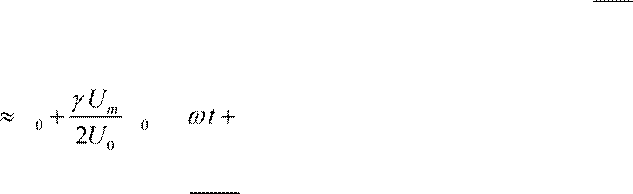v   v sin               ...

γU^m

Обозначив  за v₁ =  v ₀ коэффициент стоящий перед синусом 2U₀

получим:

v = +v₀                   v sin₁ ωt - модулированный по скорости поток электронов

Методымодуляции е-потока

1.  Метод дрейфа

2.  Метод тормозящего поля

Модуляцияе-потока по плотности. Метод дрейфа

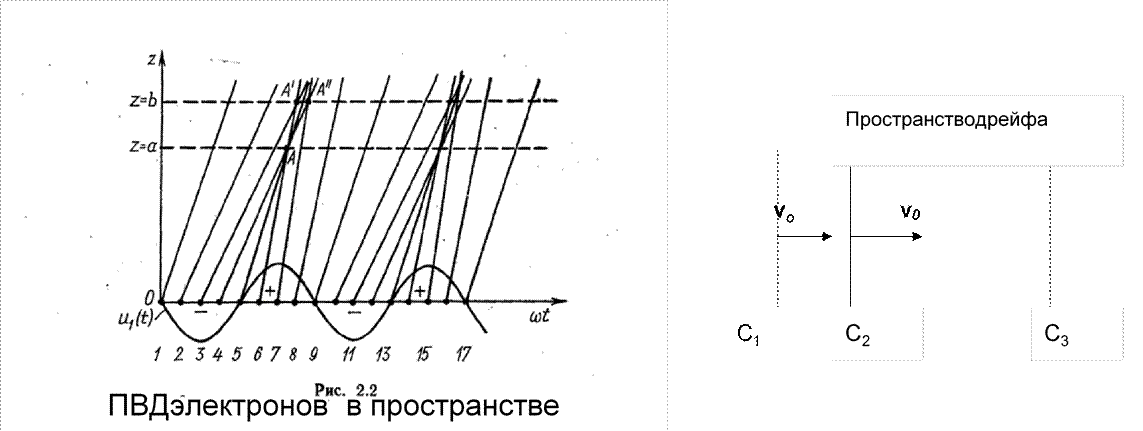
дрейфа

Модуляцияе-потока по плотности. Метод тормозящего поля

Электронныеприборы СВЧ

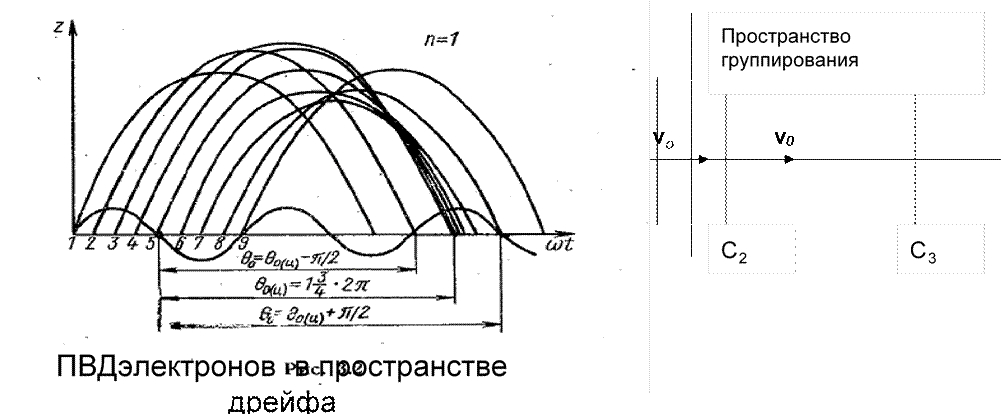
z Процессы в приборах СВЧ z модуляции по скорости z модуляции по плотности z переходу энергии электронных сгустков в СВЧ энергию

Пролетныеклистроны

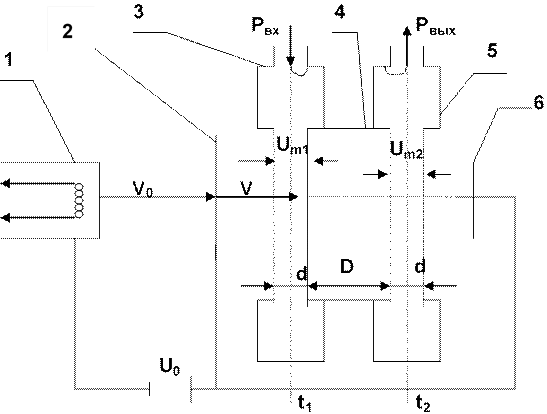
Рис.1.17.   Двухрезонаторный пролетный  клистрон

1 – катод; 2 – ускоряющий  электрод; 3 – входной  резонатор; 4 – трубка  дрейфа;  5 – выходной  резонатор; 6 – коллектор;  t1 – момент  времени, определяющий  пролет электронов через центр первого  зазора;  t2 – время пролетa электронов через второй зазор.

Математическоеописание работы клистрона

v = v₀ + v₁ sinωt₁ , где γUm

v1 =v 0

2U₀

Отношение

(U^m1)

γ  = M - называют коэффициентом модуляции электронного    2U₀

потока       

Скорость на выходе зазора:

⎛        U               ⎞

v = v0 ⎜⎜1+_γ 2U^m1 sinωt⎟⎟= v0(1+ M sinωt)           

⎝             0          ⎠

Тогда время пролета через середину вторго резонатора:

D t₂ = +t₁ , где D-расстояние между резонаторами                    v₀ + v sin₁ ωt₁

Считая v <<v _{1        0} и раскладывая в ряд по малому параметру, получим:

                               D    Dv1

t2 ≈ +t1 − 2 sinωt1 v0 v0

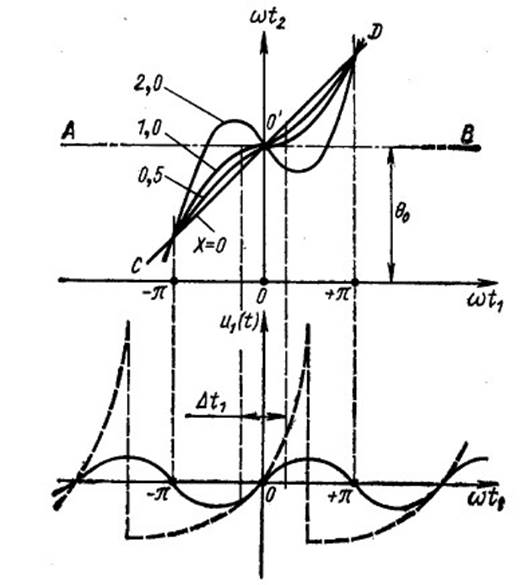Домножим на ω:

                           D           ωDv¹

ω ω ωt₂-       = t₁-( ₂             )sin(ωt)  v0 v 0

ωDv¹

Введем параметр Х=   ₂  : v 0

ω θ ωt₂- ₀= t -Xsin₁               (ωt₁)  ω γD        U^m

X=  ×   =θ₀M v0       2U0

X- называют параметром группировки

Конвекционныйток

Закон сохранения заряда dq₁  = dq₂ отсюда

i dt = i dt_{1 1          2 2}

Ток во втором резонаторе:

dt1              I0

i₂ = i₁          =

                       dt2         dt dt2 1

I - ₀ ток поступающий из эл. пушки. dt₂           ωD⋅v₁

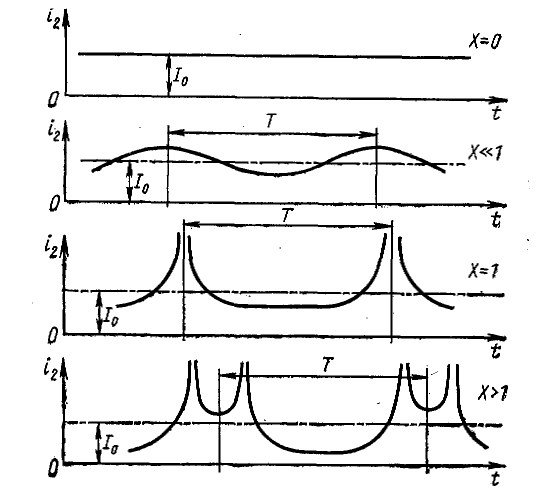
=1− ₂ cosωt₁ =1− X cosωt₁  dt1             v0

I0

i₂ =

1− X cosωt

Гармоникиконвекционного тока

При разложении в ряд фурье i , ₂ получим

i        I       I       J       nX                                n t

n=1 где n-номер гармоники, J (_n nX ) - функция Бесселя первого рода n-го порядка от аргумента nX Амплитудное значение гармоник:

I( )n = 2Jn(nX )I0

Максимум первой гармоники будет наблюдаться при при максимуме функции Бесселя J (X) ₁            при X=1,84.

Наведенныйток

Запишем уравнение наведенного тока для первой гармоники:

D d+ ₂ /2

i_нав I t        dz

d2 D d− ₂ /2

Проинтегрировав получим: iнав(1) = Iнав(1) cos(ω θt − 0 )

sinθ2 /2

где Iнав(1) =γ γ2 (1)I , 2 = ,θ ω θ ω2 = d v/ 0, 0 = D v/ 0 θ₂ /2

т.к θ₂ ≠ 0, то γ₂ ≠ 0 следовательно I_нав(1) < I₁ Для произвольной гармоники: