Ключевые слова: социальная сеть, граф, вершины графа, транзитивность сети.
MATHEMATICAL FOUNDATIONS OF MODELING SOCIAL NETWORKS
Scientific Supervisor – А.А. Gorodov
Руководитель по иностранному языку –
Siberian State Aerospace University named after academician M. F. Reshetnev, Krasnoyarsk, Russian Federation, е-mail: vasilina-petrova@mail.ru
Аннотация статьи
Преведены примеры социальных сетей. Рассмотрены проводимые ранее эксперементы. Рассмотрены общи свойства различных видов сетей, описывающих процессы в сложных социальных системах.
Keywords: social network graph, vertex transitivity network.
В настоящее время практически от каждого человека можно услышать такое словосочетание как, социальная сеть. Во второй половине XX в. это понятие начало активно использоваться на Западе при исследованиях социальных связей и человеческих отношений. Примеры социальных сетей: 1. Контакты между отдельными людьми (личные, онлайновые, деловые, профессиональные, криминальные и д.р.); 2. Сети совместной деятельности (соавторство научных статей, съёмка в одном фильме, членство в онлайн-сообществах и д.р.).
В 1969 году американскими психологами Стэнли Милгрэмом и Джеффри Трэверсом (Jeffrey Travers) была выдвинута «теория шести рукопожатий» о том, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых, в среднем состоящую из пяти человек. В разные года были проведены разные эксперименты, подтверждающие эту теорию. В 1967 эксперимент Стэнли Милгрома (“small world experiment”). Случайно выбранным жителям Омахи (Небраска) и Уичиты (Канзас) предлагалось переслать письмо адресату в Бостоне, используя только личные знакомства. Из 296 писем 64 достигли цели. Длина цепочки варьировалась от 2 до 10. Средняя длина цепочки – около 6. В 2003 был повторен эксперимент Милгрома, но с использованием электронной почты. Средняя длина цепочки около 6. Большой процент потери. В 2006 Исследовали сеть Youtube, Orkut и Flickr, средняя длина 4,25-5,88, диаметр графа 9-27. В 2011 исследовали Facebook, среднее расстояние 4.74.
Для описания моделий социальных сетей используються такие понятия как:
· Расстояние между двумя вершинами.
· Диаметр графа.
· Степень вершины (это число ребер соединенных с заданной вершиной).
· Распределение степеней вершины.
· Меры центральности узла(closeness centrality и betweenness centrality).
· Распределение меры центральности.
· Коэффициент кластеризации.
· Коэффициент ассортативности и д.р.
В случайном большом графе каждое ребро
присутствует или отсутствует с равной вероятностью и распределения степени
вершин биномиальное или пуассоновское. Далекие от распределении Пуассона
распределения степени вершин в большинстве сетей искажены со скосом вправо -
распределения имеют длинную правую хвостовую часть значений. При этом часть
вершин в сети, которые имеющие степень k – определяются
как pk. Для решения этой проблемы определения распределения
степени вершин данные о степени представляют формированием кумулятивной функции
распределения: 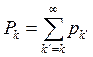 , которая
является вероятностью того, что степень ≥ k .
, которая
является вероятностью того, что степень ≥ k .
D. Watts и S. Strogatz (1998) указали, что большинство сетей имеют высокую транзитивность, называемую кластеризацией. Присутствие связей между вершинами A и B, и между B и C приводит к связи между A и C. Иначе: если B имеет двух соседей по сети A и C, то они связаны с другом друга на основании их общей связи с B. В топологических терминах: существует высокая плотность треугольников ABC (в сети) и кластеризация может быть определена количественно, измерением этой плотности:
C(1) = 3× (число треугольников на графе)/(число связных троек вершин), где "связная тройка" – вершина, соединенную непосредственно с неупорядоченной парой других вершин. Фактически, C измеряет часть троек, которые имеют третье ребро для формирования треугольника. Множитель "3" приведен для учета того, что каждый треугольник входит в три тройки, поэтому 0≤C≤1.
Альтернативное определение индекса кластеризации (Watts and Strogatz, 1998) следующее:
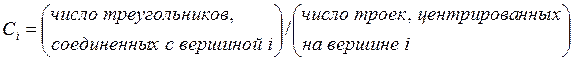 .
.
Для вершин со степенью 0 или 1: Ci = 0 . Тогда индекс кластеризации в среднем по сети:
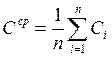 .
.
В теории моделирования социальных сетей на данном этапе сформировались три основных направления:
1. Нахождение статистических свойств, которые характеризуют поведение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.