Надежность программного обеспечения. Аналитические модели надежности. Модель «дискретно-понижающая интенсивность проявления ошибок»

ЛЕКЦИЯ № 3 НАДЕЖНОСТЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

Аналитические модели надежности

• Аналитическое моделирование надежности программного средства включает четыре шага:
• определение предположений, связанных с процедурой тестирования программного средства;
• разработка или выбор аналитической модели, базирующейся на предположениях о процедуре тестирования;
• выбор параметров моделей с использование полученных данных;
• применение модели - расчет количественных показателей надежности по модели.

ЛЕКЦИЯ 3

2

Аналитические динамические модели надежности

• Рассмотрим следующие аналитические динамические модели:
• Дискретно-понижающая интенсивность проявления ошибок.
• Шумана.
• Джелинского-Моранды.

ЛЕКЦИЯ 3

3

Модель «дискретно-понижающая интенсивность проявления ошибок»

В этой модели предполагается, что интенсивность обнаружения ошибок описывается кусочно-постоянной функцией, пропорциональной числу не устраненных ошибок, т.е. интенсивность отказов λ(t) постоянна до обнаружения и устранения ошибки, после чего она опять становится константой, но с другим, меньшим значением. При этом предполагается, что между λ(t) и числом оставшихся в программе ошибок существует зависимость λ(t) = K(M-i) = λ где М - неизвестное первоначальное число ошибок; i - число обнаруженных ошибок, зависящее от времени t; К- некоторая констант

ЛЕКЦИЯ 3

4

Модель «дискретно-понижающая интенсивность проявления ошибок» (продолжение)

Зависимость интенсивности отказов программы от времени

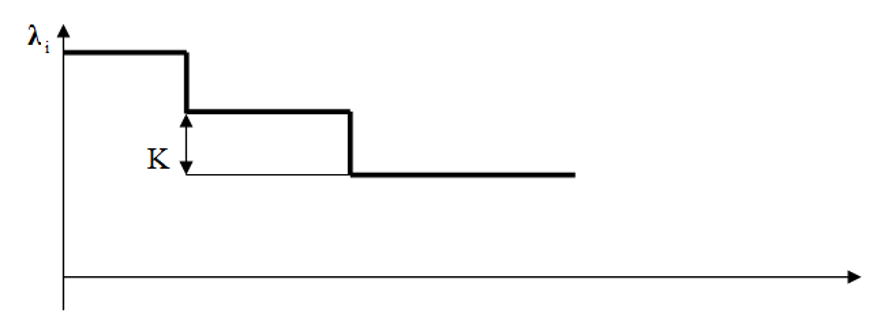
Каждый раз, когда ошибка обнаруживается, (модель предполагает, что задержка между обнаружением ошибки и ее исправлением отсутствует) λ(t) уменьшается на некоторую величину К

ЛЕКЦИЯ 3

5

Модель «дискретно-понижающая интенсивность проявления ошибок» (продолжение)

Плотность вероятности обнаружения i-той ошибки на интервале времени t задается соотношением f(t) = λexp(-λ t ) = K(M-i) exp (-K(M-i) t ) Неизвестные параметры К и М можно оценить, если некоторое количество ошибок уже обнаружено (например, если фаза тестирования уже частично пройдена).

ЛЕКЦИЯ 3

6

Модель «дискретно-понижающая интенсивность проявления ошибок» (продолжение)

Предположим, что обнаружено m ошибок, а t[1],t[2],…,t[m] интервалы времени между этими ошибками. Тогда значения неизвестных параметров К и М может быть оценено на основании последовательности наблюдений интервалов между моментами обнаружения ошибок по методу максимального правдоподобия. При этом для нахождения оценок параметров К и М необходимо решить следующие уравнения:

Получилось два уравнения с двумя неизвестными K и M следовательно, их можно решить и найти значения M и K.

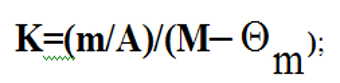
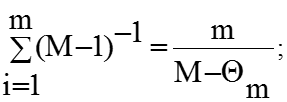
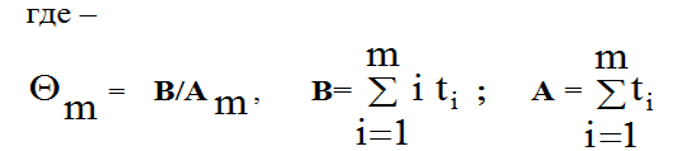
ЛЕКЦИЯ 3

7

Модель «дискретно-понижающая интенсивность проявления ошибок» (пример)

Пусть m=10 (десять обнаруженных ошибок) с интервалами между отказами (в минутах) 9, 17, 21, 54, 32, 78, 82, 33, 57, 82 по модели можно сосчитать, что осталось 3,3 ошибки (M=13,3). Интервалы времени между 10 11 12 и 13 ошибками оцениваются в 135, 245 и 1265 минут.

ЛЕКЦИЯ 3

8

Оценка модели «дискретно-понижающая интенсивность проявления ошибок»

Эта модель надежности программ является достаточно грубой. На практике часто не соблюдаются условия, на которых она построена: – не всегда при устранении ошибки интенсивность отказов уменьшается на одну и ту же величину K, так как разные ошибки имеют различное влияние на ход исполнения программы; – довольно часто возникают ситуации, при которых устранение одних ошибок приводит к появлению новых; – не всегда удаётся устранить причину ошибки и программу продолжают