Scale-free topology of e-mail networks. For the Poissonian distribution of a random network

architectures.

PACS numbers: 89.20.Hh, 89.75.Hc, 05.65.+b

Complex networks as the World Wide Web or social networks often do not have an engineered architecture but instead are self-organized by the actions of a large number of individuals. From these local interactions nontrivial global phenomena can emerge as, for example, small-world properties [1] or a scale-free distribution of the degree [2]. These global properties have considerable implications on the behavior of the network under error or attack [3], as well as on the spreading of information or epidemics [4]. Here we report that networks composed of persons connected by exchanged e-mails show both the characteristics of small-world networks and scale-free networks.

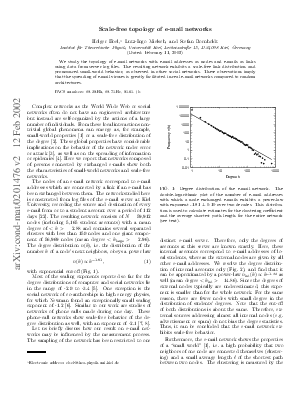
The nodes of an e-mail network correspond to e-mail addresses which are connected by a link if an e-mail has been exchanged between them. The network studied here is constructed from log files of the e-mail server at Kiel University, recording the source and destination of every e-mail from or to a student account over a period of 112 days [22]. The resulting network consists of N = 59,912 nodes (including 5,165 student accounts) with a mean degree of < k > = 2.88 and contains several separated clusters with less than 150 nodes and one giant component of 56,969 nodes (mean degree < k_large > = 2.96). The degree distribution n(k), i.e. the distribution of the number k of a node’s next neighbors, obeys a power law

                                        n(k) ∝ k^−1.81,                                   (1)

with exponential cut-off (Fig. 1).

Most of the scaling exponents reported so far for the degree distributions of computer and social networks lie in the range of -2.0 to -3.4 [5]. One exception is the social network of co-authorships in high energy physics, for which Newman found an exceptionally small scaling exponent of -1.2 [6]. Similar to our work are studies of networks of phone calls made during one day. These phone-call networks show scale-free behavior of the degree distribution as well, with an exponent of -2.1 [7, 8]. Let us briefly discuss how our result on e-mail networks may be influenced by the measurement process. The sampling of the network has been restricted to one

FIG. 1: Degree distribution of the e-mail network. The double-logarithmic plot of the number of e-mail addresses with which a node exchanged e-mails exhibits a power-law with exponent -1.81 ± 0.10 over two decades. This distribution is used to calculate estimates for the clustering coefficient and the average shortest path length for the entire network (see text).

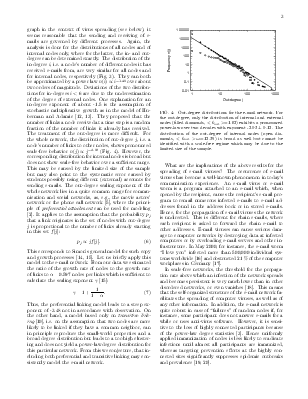
distinct e-mail server. Therefore, only the degrees of accounts at this server are known exactly. Here, these internal accounts correspond to e-mail addresses of local students, whereas the external nodes are given by all other e-mail addresses. We resolve the degree distribution of internal accounts only (Fig. 2), and find that it can be approximated by a power-law n_int(k) ∝ k^−1.32 as well (mean degree < k_int >= 14.86). Since the degrees of external nodes typically are underestimated, this exponent is smaller than for the whole network. For the same reason, there are fewer nodes with small degree in the distribution of students’ degrees. Note that the cut-off of both distributions is about the same. Therefore, external sources addressing almost all internal nodes (e.g. advertisement or spam) do not bias the degree statistics. Thus, it can be concluded that the e-mail network exhibits scale-free behavior.

Furthermore, the e-mail network shows the properties of a “small