Методы линейной теории (Интеграл Фурье)

ЛЕКЦИЯ 6

3.4. Интеграл Фурье

До сих пор мы применяли разложение на синусоидальные составляющие   только  к  периодическим  функциям,  представляя  их  рядами   Фурье.

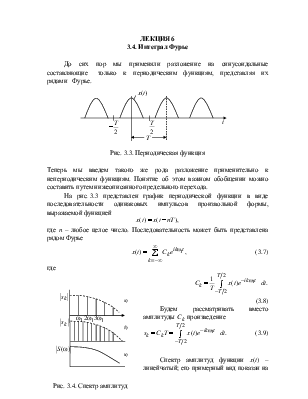
Рис. 3.3. Периодическая функция

Теперь мы введем такого же рода разложение применительно к непериодическим функциям. Понятие об этом важном обобщении можно составить путем нижеописанного предельного перехода.

На рис. 3.3 представлен график периодической функции в виде последовательности одинаковых импульсов произвольной формы, выражаемой функцией

где n – любое целое число. Последовательность может быть представлена рядом Фурье

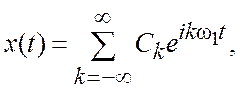                                         (3.7)

где

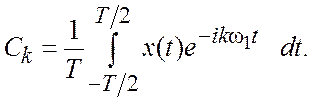                                    (3.8)

Будем рассматривать вместо амплитуды  произведение

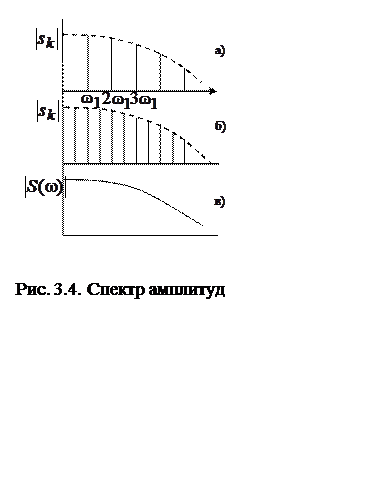
                 (3.9)

Спектр амплитуд функции x(t) – линейчатый; его примерный вид показан на рис. 3.4, а; спектр построен в масштабе  (а не ) по оси ординат. Расстояния между спектральными линиями по оси абсцисс равны .

Будем теперь увеличивать Т. При этом интервал между спектральными линиями соответственно уменьшится. Однако для тех же значений , что и прежде, значение  останется неизменным, как это видно из формулы (3.9). Поэтому, если, например, период увеличился вдвое, то число линий удваивается, причем первоначальные линии спектра сохраняют свою величину и положение, а между ними появляются новые, как показано на рис. 3.4, б. Так как  для некоторой частоты  остается неизменным, то это значит, что амплитуда  убывает с увеличением периода Т. Если продолжать увеличивать период, то линейчатый спектр будет становиться все более густым. При переходе к пределу при  интервал между линиями будет стремиться к нулю, и совокупность дискретных точек с координатами  превратится в непрерывную последовательность точек, т.е. в линию, представляющую некоторую непрерывную функцию частоты, которую мы обозначим  (рис. 3.4, в). Но при неограниченном увеличении периода периодическая последовательность рис. 3.3 вырождается, и переходит в один единственный импульс, представляемый функцией x(t). Таким образом, устремляя Т к бесконечности, мы переходим в пределе от периодической функции к непериодической.

Выразим амплитуду  как

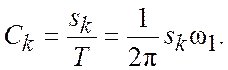
Но при  величина ω₁, представляющая собой интервал между линиями, превращается в , а  переходит в непрерывную функцию . Заменяя в (3.7) сумму интегралом, получаем

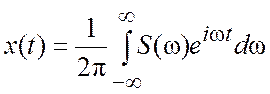.                                     (3.10)

Это и есть интеграл Фурье. Он позволяет любую (с некоторыми математическими ограничениями) непериодическую функцию представить в виде суммы бесконечного числа синусоидальных колебаний с бесконечно малыми амплитудами  и с бесконечно малым интервалом  по частоте. Говорят, что в составе непериодической функции имеются «все частоты». Функция  выражает спектральную плотность комплексной амплитуды. Она определяется на основании формулы (3.9), в которую вместо дискретных значений частоты  нужно ввести непрерывно изменяющуюся (текущую) частоту :

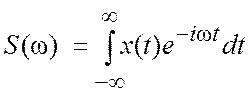.                                          (3.11)

Формула (3.11) позволяет найти  по заданному , а формула (3.10) –  по заданному . Формулы (3.10) и (3.11) имеют симметричное строение и называются парой преобразований Фурье.

Функция  – комплексная функция; она содержит сведения, как о спектре амплитуд, так и о спектре фаз. Мы будем в дальнейшем называть функцию  для краткости комплексным спектром. Ее модуль

дает сведения только о частотном распределении амплитуды. Во многих случаях только это нас и интересует. Мы будем называть функцию Ф(ω) просто спектром, если это не потребует оговорок.

Спектр непериодической функции, выражаемый непрерывной функцией частоты, называется сплошным (в отличие от линейчатого спектра периодической функции).

Проделанное рассуждение, приведшее нас к основным формулам (3.10) и (3.11), не является математически строгим. Однако оно дало нам попутно весьма полезный результат, а именно: мы установили связь между спектром одиночного импульса и спектром периодической последовательности, получаемой периодическим повторением импульса. Эта связь может быть выражена следующим правилом: линейчатый спектр амплитуд периодической последовательности импульсов (построенный в масштабе ) вписывается в кривую  сплошного спектра одиночного импульса. Аналогичное правило может быть сформулировано и для спектра фаз.

В качестве примера рассмотрим импульс прямоугольной формы (рис. 3.5).

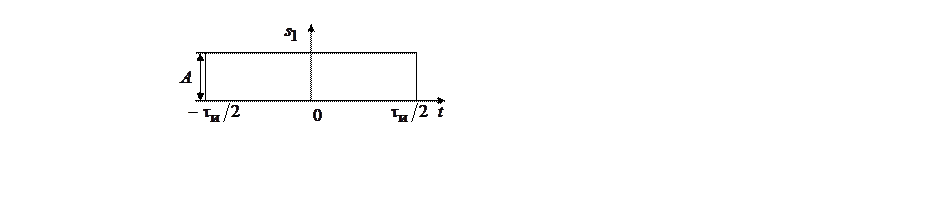
Рис. 3.5. Импульс прямоугольной формы

Простейшее колебание, определяемое выражением

,

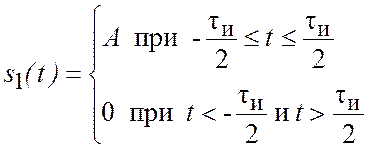и представленное на рис. 3.5, получило широкое распространение, как в технике, так и в теории сигналов и цепей. Применяя формулу (3.11) находим спектральную плотность (рис. 3.6).

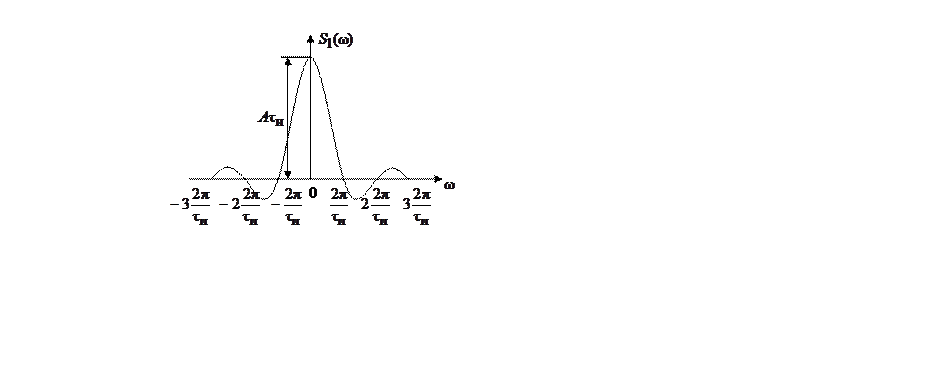
Рис. 3.6. Спектральная плотность прямоугольного импульса

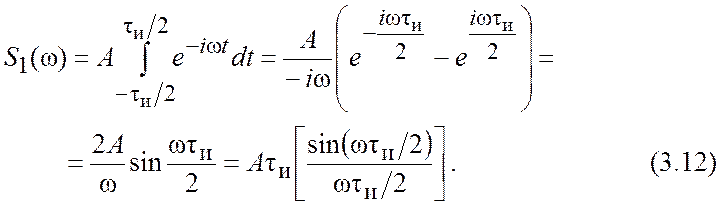
Заметим, что произведение , равное площади импульса, определяет значение спектральной плотности импульса при , т.е. . Этот вывод можно распространить на импульс произвольной формы.

Действительно, из общего выражения (3.11) следует, что

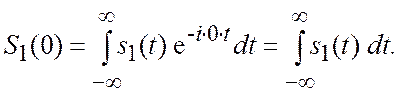
Правая часть этого выражения есть не что иное, как площадь импульса . Таким образом, выражение (3.12) можно записать в форме

.

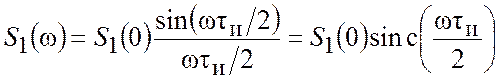Здесь через  обозначена функция

.

При удлинении (растягивании) импульса, расстояние между нулями функции  сокращается, что равносильно сужению спектра. Значение  при этом возрастает. При укорочении (сжатии) импульса, наоборот, расстояние между нулями функции  увеличивается (расширение спектра), а значение  уменьшается. В пределе при  (A = const) точки , соответствующие двум первым нулям функции , удаляются в бесконечность и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от  до .

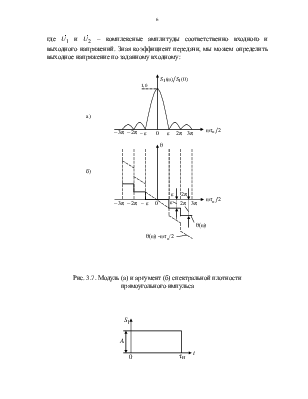
На рис. 3.7 показаны отдельно графики модуля , отнесенного к величине , и аргумента  спектральной плотности. Первый из этих графиков можно рассматривать как амплитудную, а второй – как фазовую характеристику спектра прямоугольного импульса. Каждая перемена знака  учитывается на рис. 3.7, б приращением фазы на .

При отсчете времени не от середины импульса (как на рис. 3.5), а от фронта (рис. 3.8) фазовая характеристика спектра импульса должна быть дополнена слагаемым , учитывающим сдвиг импульса на время  (в сторону запаздывания). Результирующая фазовая характеристика принимает при этом вид, показанный на рис. 3.7, б штриховой линией.

Теперь займемся вопросом о применении математического аппарата преобразований Фурье к решению основной задачи линейной системы на произвольное воздействие x(t). Основная идея состоит в том, что мы легко можем найти отклик системы на синусоидальное воздействие. Для этого достаточно знать коэффициент передачи системы, т.е. комплексное отношение

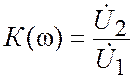,                                               (3.13)

где  и  – комплексные амплитуды соответственно входного и выходного напряжений. Зная коэффициент передачи, мы можем определить выходное напряжение по заданному входному:

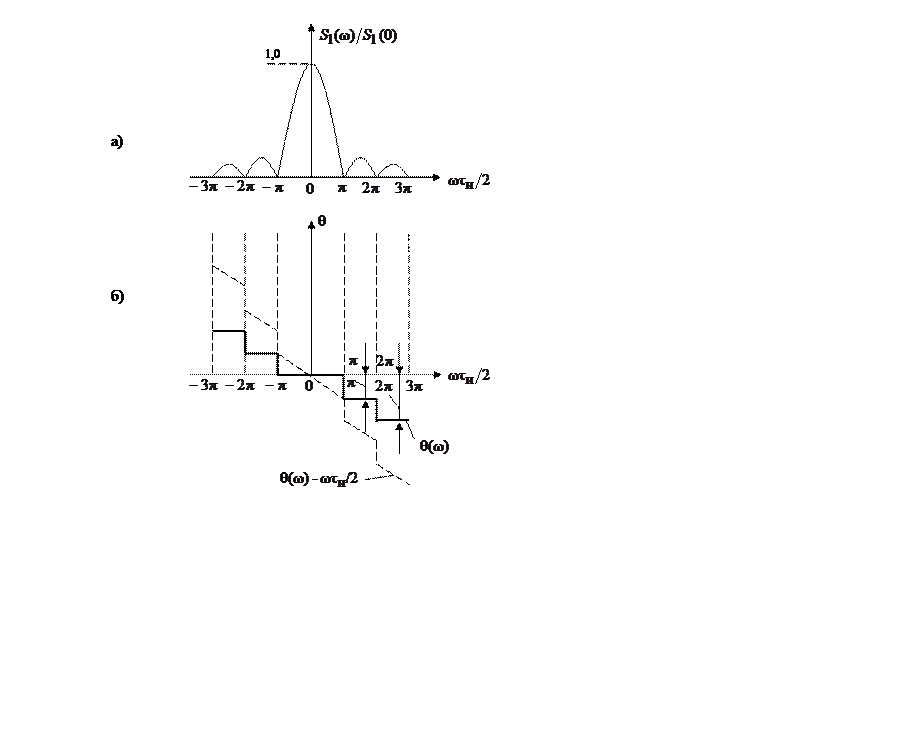
Рис. 3.7. Модуль (а) и аргумент (б) спектральной плотности

прямоугольного импульса

Рис. 3.8. Совмещение начала отсчета времени

с фронтом прямоугольного импульса

.                                             (3.14)

При таких обстоятельствах для решения задачи об отклике на произвольное воздействие x(t) удобно разложить воздействие на синусоидальные составляющие. Именно такое разложение и представляет собою интеграл Фурье (3.10):

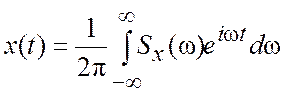.                                   (3.15)

(Мы снабдили спектр индексом x, чтобы подчеркнуть, что речь идет о спектре функции x(t)).

Отдельное бесконечно малое слагаемое воздействия x(t) имеет вид

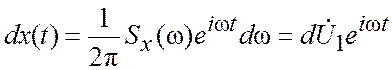,                             (3.16)

где 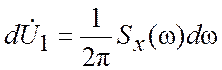  – бесконечно малая амплитуда. Отклик на синусоидальное колебание (3.16), поданное на вход, будет также синусоидальным колебанием

,

причем комплексная бесконечно малая амплитуда  на выходе определится по формуле (3.14):

Таким образом, отклик на воздействие  будет

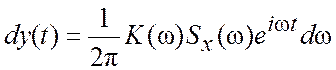.                               (3.17)

Чтобы получить полный отклик , нужно просуммировать (3.17) по всем частотам, т.е. составить (на основании принципа наложения) интеграл

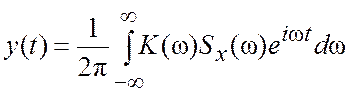.                               (3.18)

Это и есть формула для нахождения отклика линейной системы на произвольное воздействие методом интеграла Фурье.

Заметим, что функция  может быть вообще представлена интегралом Фурье следующего вида (см. формулу(3.15)):

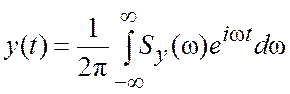.                                   (3.19)

Сопоставляя (3.18) и (3.19), получаем простое, но важное соотношение

,                                      (3.20)

т.е. спектр отклика равен спектру воздействия, умноженному на коэффициент передачи. Во многих случаях нас интересует не отклик как функция времени , а именно спектр отклика . В этих случаях формула (3.20) дает сразу нужный нам результат.

Касаясь практической стороны дела, нужно заметить, что вычисление интегралов вида (3.18) обычными методами затруднительно. Наиболее эффективно применение для этой цели метода, основанного на теореме о вычетах (из теории функций комплексного переменного). С этой точки зрения проще в применении метод интеграла наложения (свертка двух функций), описанный далее.