Разработка структурной схемы связи, предназначенной для передачи аналоговых сигналов методом ИКМ для заданного вида модуляции и способа приема сигнала, страница 5

6 Статистическое (эффективное) кодирование

Статистическое кодирование предполагает уменьшение избыточности сообщений, обусловленной неравно вероятностью элементов. Уменьшение избыточности сообщений называют так же сжатием.

Важнейшей характеристикой источника информации является энтропия – количественная оценка информации, переносимая одним битом, и определяется по формуле:

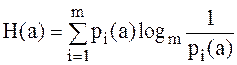 ,                   (6.1)

где m – основание кода.

Если известно вероятность ноля или единицы, то для двоичного кодирования энтропию сообщения можно записать так:

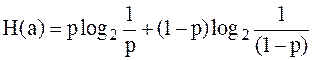,       (6.2)

По заданию вероятность появление единицы p(1) = 0,9 , по формуле 6.2 найдем H(a):

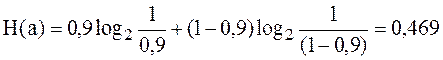 бит/символ.

Найдем коэффициент избыточности :

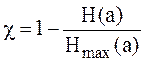,                                   (6.3)

Где  - максимальная энтропия сообщения и равна 1бит/символ, т.е. появление ноля и единицы равновероятные события:

 

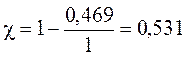
Т.к. коэффициент избыточности , то необходимо провести статистическое (эффективное) кодирование.

Суть такого кодирования заключается в следующем: для передачи информации по каналу используется некий алфавит с n числом букв (кодовых комбинаций). Появления разных букв разновероятно, поэтому возможно кодировать разные кодовые комбинации различной длиной. Статистическое кодирование проводится по методу Шеннона-Фано или Шаффмана.

Применим в нашем случае метод Хаффмана, отличие его от метода Шеннона-Фано заключается в том, что построение кода идет от наименее вероятных символов.

Запишем в столбец символы, их код и вероятность появления этих символов (таблица 6.1).

Таблица 6.1 – Расчет вероятностей знаков

Знаки	Код	Формула вероятности	Вероятность
z1	000		0,001
z2	001		0,009
z3	010		0,009
z4	011		0,081
z5	100		0,009
z6	101		0,081
z7	110		0,081
z8	111		0,729

Запишем в таблице 6.2 знаки в порядке убывания и попарно обьеденим  близко вероятные знаки.

Таблица 6.2 – Построение кода Хаффмана

Знаки	Вероятности	1	2	3	4	5	6	7
z8	0,729	0,729	0,729	0,729	0,729	0,729	0,729	1
z4	0,081	0,081	0,081	0,081	0,109	0,162	0,271
z6	0,081	0,081	0,081	0,081	0,081	0,109
z7	0,081	0,081	0,081	0,081	0,081
z2	0,009	0,01	0,018	0,028
z3	0,009	0,009	0,01
z5	0,009	0,009
z1	0,001

По таблице 6.2 построим граф для построения кода (рисунок 6.1). По данному графу запишем в таблице 6.3 полученные коды знаков и их длины.

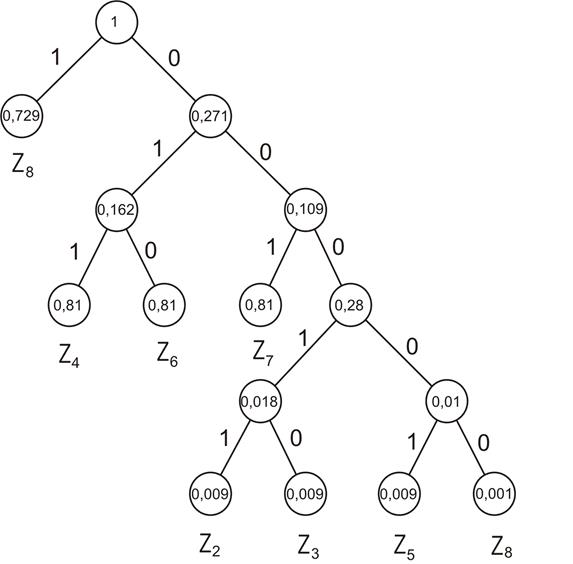
Рисунок 6.1 – граф кода Хаффмана

Таблица 6.3 – К расчету эффективной энтропии сообщения