




















стоимость МКС меньше, чем прокладка линии, а стоимость соединительных линий составляет около 90% от стоимости станции, то использование блока 80 х 120 х 400 экономичнее, чем блок 60 х 80 х 400.
На вход ступени БСЛ АТСКЭ поступает нагрузка по двум пучкам линий, математическое ожидание которого У1 и У2. На входе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам Кi.
Определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам сделать вывод. Исходные значения У1= 65 эрл, У2=15 эрл , K1=0.2,
K2=0.2, K3 =0.25, K4=0.35
Так как в различные дни, недели, месяцы, годы в ЧНН нагрузка изменяется постоянно, то это изменение приводит к изменению качественных показателей качества обслуживания, которые ухудшаются. Чтобы качественные показатели не превышали заданных значений, необходимо использовать такую нагрузку, при которой с максимальной вероятностью качественные показатели оставались постоянными. Такой нагрузкой является расчетная нагрузка, которая учитывает колеблемость нагрузки, поступающей на пучок соединительных устройств.
Значение расчетной нагрузки определяется по формуле
![]() (7.1), где У-
математическое ожидание нагрузки.
(7.1), где У-
математическое ожидание нагрузки.
В данном случае У=У1+У2 = 85 эрл.
Следующим этапом необходимо распределить эту нагрузку по направлениям, в соответствии с коэффициентами направления, по формуле
![]()
Далее определим расчетную нагрузку Ур по формуле (7.1)
![]()
![]()
![]()
Определим математическое ожидание нагрузки данного направления по формуле
![]() Эрл
Эрл
![]() Эрл
Эрл
![]() Эрл
Эрл
![]() Эрл
Эрл
По полученным данным следует рассчитать величину относительного отклонения расчетной нагрузки от ее математического ожидания по формуле
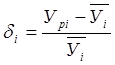
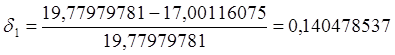
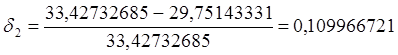
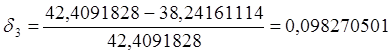
Вывод.
При малых нагрузках относительные колебания качественных параметров максимальны, а при больших нагрузках изменяются незначительно. Поэтому характеристики системы более стабильны.
С увеличением нагрузки, величина относительного отклонения более стабильна и соответственно влияния на качественные характеристики коммутационной системы будут менее заметны, в отличие от систем с малыми нагрузками.
Заключение.
В данной курсовой работе был проведен ряд вычислений по некоторым областям применения математических моделей теории телетрафика (коммутационные системы, потоки вызовов, характеристики качества обслуживания, время обслуживания) и сделаны выводы по выполненным расчетам.
Целью первой задачи является закрепление материала по изучению математических моделей простейшего и примитивного потоков вызовов. Получив графическую зависимость вероятности поступления вызовов от числа источников, можно сделать вывод, что при увеличении числа источников простейший поток стремиться к примитивному.
Цель второй задачи заключается в расчете нагрузки поступающей на БАИ. Величина нагрузки прямо пропорционально зависит от числа источников нагрузки, непроизводительной нагрузки α , среднего числа вызовов от одного источника С. При заданных условиях значение нагрузки получилось равным У= 246,1157511 Эрл
В третьей задаче рассматривалась зависимость пропускной способности полнодоступного пучка линий от характера поступающего потока вызовов. При уменьшении числа источников в примитивном потоке нагрузка увеличивается (при N=20 У=0,8 Эрл, а при N= 10 У=0,9 Эрл) и стремиться к нагрузке простейшего потока (У=0,9 Эрл). Незначительное увеличение нагрузки приводит к значительному увеличению потерь, но несмотря на это требуется меньшее число соединительных линий, что увеличивает эффективность использования соединительных линий, уменьшает затраты, но качество обслуживания при этом уменьшается.
В четвертой задаче определяли основные качественные показатели работы приборов управления АТСК. В данной задаче были рассчитаны: среднее время ожидания вызова tз=0,35с и вероятность ожидания свыше времени t P(g>t)=0.0031 при t = с.
Пятая задача решается при помощи метода О’Делла. При заданной доступности (d=12) определено число выходов (V1 = 30,25, V2= 27,02) неполнодоступной системы, требуемых для обслуживания заданной нагрузки (У = 17 Эрл) при установленном качестве обслуживания, определена оптимальная структура неполнодоступной схемы. Также из расчетов видно, что при увеличении потерь емкость пучка уменьшается (в данном случае – на 3 линии) это приводит к эффективному использованию соединительных линий.
Шестая задача решалась с помощью метода эффективной доступности. В данной задаче были вычислены емкости пучка линий для блоков В данной задаче были вычислены емкости пучка линий для блоков 60 x 80 x 400 и 80 x 120 x 400. Из расчетов видно, что при одинаковой величине нагрузки емкость пучка для этих блоков различна. Таким образом эффективнее использовать блок 80 х 120 х 400, так как здесь используется меньшее число линий V = 64, чем в блоке 60 х 80 х 400 при V = 66 – разница в две линии. Так как стоимость МКС меньше, чем прокладка линии, а стоимость
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.