Работа № 5 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ
Введение
Выбор метода измерения сопротивления постоянному току и соответствующей аппаратуры зависят от величины измеряемого сопротивления, требуемой точности и. условий, в которых производится измерение.
Если, например, при измерении сопротивлений измерительных катушек или сопротивлений шунтов требуется точность порядка сотых и даже тысячных долей процента, то при измерении сопротивления изоляции погрешность порядка 10-15% является вполне допустимой.
Наиболее простые методы измерения и наиболее простая аппаратура позволяют сравнительно быстро, в любых условиях, но с относительно невысокой точностью (до единиц или десятых долей процента) производить измерения сопротивлений в широком диапазоне*. Сюда относятся метод амперметра и вольтметра, приборы с непосредственным отсчетом омметры и мегомметры и т. д.
Более сложными, обычно лабораторными, являются методы сравнения измеряемого сопротивления с образцовыми. Сюда относятся, в первую очередь, компенсационные и мостовые методы, позволяющие получать наибольшую точность измерения.
Специальные методы измерения сопротивлений (метод заряда и разряда конденсатора и др.) в настоящей работе не рассматриваются.
Целью настоящей работы является ознакомление с некоторыми наиболее распространенными методами и приборами для измерения сопротивления постоянному току в диапазоне от 10–8 до 1014 Ом.
* В электротехнике условно принята следующая классификация сопротивлений по величине:
а) малые сопротивления — до 1 ом,
б) средние сопротивления — от 1 до 105 ом;
в) большие сопротивления — от 106 и выше.
I. Измерение сопротивлений с помощью мостов постоянного тока
Мостовые методы измерения сопротивлений являются наиболее точными методами измерения малых и средних сопротивлений.
Наибольшее распространение в электроизмерительной технике полечили одинарные (четырехплечие) мосты для измерения среднихсопротивлений и двойные мостыдляизмерения малых сопротивлкний Требования к мостам постоянного тока нормированы государственным стандартом — ГОСТ 7165-66 (выписки из этого ГОСТа приведены на стенде).
а) Одинарный мост.
Схема одинарного моста представлена на рис. 5-1. Четыре сопротивления Rx ; R1 R2и Rз называются плечами моста. В одну из диагоналей (ас) включен источник питания, обычно аккумуляторная батарея Б. Во вторую диагональ (bd) включен нулевой прибор, обычно магнитоэлектрический гальванометр — G.
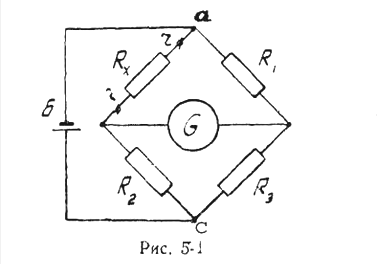
Как известно, для того, чтобы мост был уравновешен, то есть, чтобы ток в гальванометре был равен нулю, необходимо выполнить следующее условие: RxR3=R1R2
Измеряемое сопротивление Rxможет быть вычислено по известным значениям остальных трех сопротивлений, при которых имеет место равновесие моста
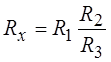. (5-1)
Плечо R1называют плечом сравнения, а плечи R2и R3— плечами отношения.
Нижний предел измерения четырехплечего моста ограничен тем, что при малом измеряемом сопротивлении Rx большую погрешность в измерение вносят последовательно с ним включенные сопротивления соединительных проводов и контактов. Для иллюстрации влияния сопротивления соединительных проводов рассмотрим следующий пример.
Допустим, что величина измеряемого сопротивления равна. 1 ом. Сопротивление каждого из проводников, подсоединяющих искомое сопротивление к мостовой схеме (рис. 5-1), составляет r=0,01 ом.
Тогда сопротивление, измеряемое мостом, будет равно Rx+2г, а относительная погрешность, вносимая соединительными проводами, может быть определена следующим образом:
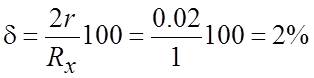
В ряде случаев такая ошибка является недопустимой. При меньших величинах измеряемого сопротивления погрешность при измерении одинарным мостом может достигнуть десятков процентов, то есть привести к практической невозможности произвести измерение.
Для измерения сопротивления порядка 1010¸1012 ом и выше обычно мосты непригодны.
При таких значениях измеряемых сопротивлений сопротивление утечки между зажимами, к которым присоединяется неизвестное сопротивление Rx(сопротивление диэлектрика, на котором смонтированы входные зажимы моста), может оказаться соизмеримым с ним и резко исказить результат измерения.
Следует также иметь в виду, что по мере увеличения измеряемого сопротивления ухудшается чувствительность моста. Для увеличения чувствительности моста следует повысить напряжение питания, что можно сделать только в известных пределах.
б) Двойной мост.
Для измерения малых сопротивлений, для которых, как было указано выше, применение одинарного моста не может дать точных результатов, наиболее широкое распространение получили двойные мосты.
Принципиальная схема двойного моста представлена на рис. 5-2.
На этой схеме Rx— измеряемое сопротивление; RN— образцовое сопротивление, R1; R’1; R2и R3— известные сопротивления.
Для увеличения точности измерения малке сопротивления как измеряемые, так и образцовые обычно делаются четырехзажимными. Одна пара зажимов (так называемые «токовые») служит для включения сопротивления в цепь основного тока. Проводники от второй пары зажимов («потенциальных») подсоединяются к соответствующим зажимам моста. Таким образом, собственно величиной измеряемого (или, соответственно, образцового) сопротивления является сопротивление между потенциальными зажимами. Такая четырехзажимная конструкция уменьшает влияние переходных сопротивлений токовых зажимов на результат измерения.
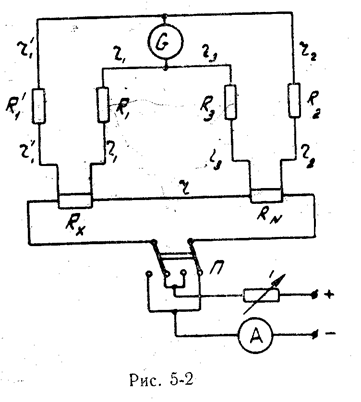
Чтобы получить значение измеряемого сопротивления, необходимо вывести уравнение равновесия двойного моста. Это нетрудно сделать путем трансфигурации треугольника сопротивлений R1, R3 и r (рис.5-2 ) в эквивалентную звезду, после чего получается схема простого одинарного моста (r— сопротивление между внутренними потенциальными зажимами сопротивлений Rx и RN ). Можно также составить для схемы рис.5-2 на основе законов Кирхгофа систему уравнений, решение которой относительно Rx даст искомое уравнение.
Пользуясь любым из указанных методов, нетрудно получить уравнение равновесия моста в следующем виде:
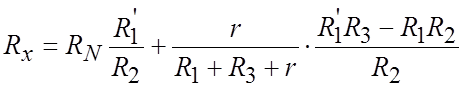. (5-2)
Практически пользоваться этим уравнением для определения Rх нельзя, так как, во-первых, уравнение слишком неудобно и сложно для расчетов, а, во-вторых, входящее в (5-2) сопротивление r неизвестно и может быть оценено только весьма приближенно. Поэтому, чтобы упростить выражение (5-2) и уменьшить по возможности влияние r, стараются выполнить условия, при которых величина второго члена выражения (5-2) будет столь мала, что ею можно без ущерба для точности измерения пренебречь. Нетрудно видеть, что в первую очередь для этого следует обеспечить равенство нулю выражения:
R/1R3–R1R2=0. (5-3)
При этом второй член выражения (5-2) обращается в нуль и
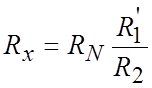. (5-4)
Чтобы выполнить условие (5-3), обычно в двойных мостах делают
R1 = R/1 (5-5)
R2 = R3 (5-6)
Таким образом, при уравновешивании двойного моста обеспечивают выполнение двух условий
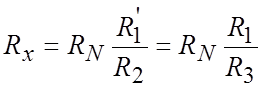(5-7)
то есть достигают двойного равновесия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.