Расчет параболической однозеркальной антенны. Диаграмма направленности пирамидального рупора. Расчет коэффициента направленного действия, страница 3

Далее рассчитывается фокусное расстояние:

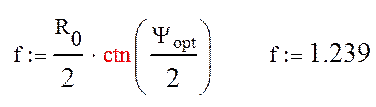
которое нужно откорректировать с тем, чтобы выполнялось равенство

уточняем фокусное расстояние

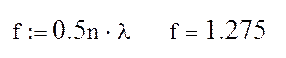
Форма сечения параболического зеркала рассчитывается по формуле:

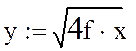
Подставляя вместо х значения от 0 до 5 с шагом 0,5 получаем результаты, которые заносим в таблицу 3.

  Таблица 3.

x	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5
y	0	1,597	2,258	2,766	3,194	3,571	3,912	4,225	4,517	4,791	5,05

Часть отраженных от зеркала лучей на пути которых расположен облучатель, перехватывается этим облучателем. Для устранения отраженной от вершины зеркала электромагнитной волны, которая, попадая в тракт питания, ухудшает КБВ, ставится компенсирующая пластина диаметром d на расстоянии t.

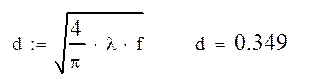
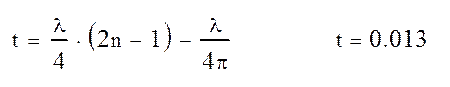
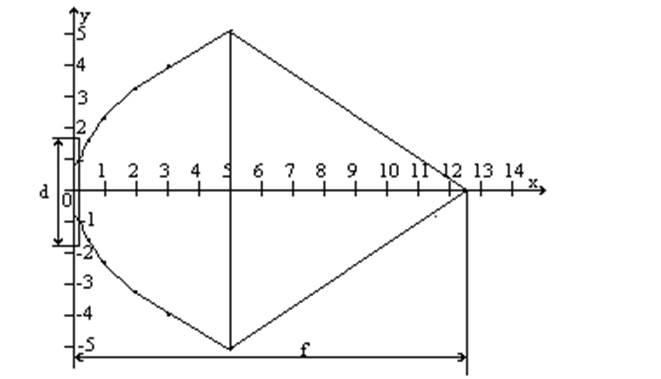
Рис. 8

5.  Расчет диаграммы направленности антенны

Поле излучения создаваемое зеркалом можно найти, зная наведенный облучателем на его поверхности ток. Вместо тока на «освещенной» стороне зеркала можно рассматривать поле в плоскости раскрыва, которое изменяется электрическими и магнитными эквивалентными поверхностными токами, либо распределением источников типа элемента Гюйгенса. Отсюда два метода расчета направленности излучения антенны: токовый и апертурный (по полю). Однако в обоих методах предполагается, что каждый элемент зеркала действует как элемент плоскости, что дает лишь приближенный результат. Распределение тока по поверхности зеркала вычисляют по известной характеристике направленности облучателя. На всех этапах расчета вводится предположение, упрощение и т.п., поэтому расчетные формулы для ДН являются приближенными. ДН антенны определяется: ДН облучателя, амплитудным и фазовым распределениями в раскрыве антенны, отношением геометрических размеров к длине волны.

Для расчета ДН антенны с пирамидальным рупорным типом облучателя применим общий метод расчета. Характеристика направленности этой антенны выражается формулой:

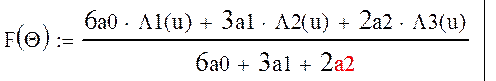
где

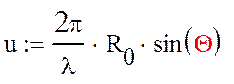
 - лямбда функции от аргумента u

Расчет коэффициентов а0, а1, а2:

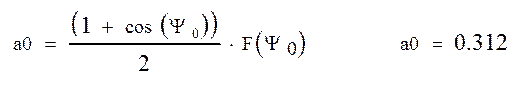
Решим систему уравнений:

     а0+а1+а2=1

     а0+а1(1- R1²) + a2(1- R1²)² = F(R1)

a0 = F(1)

R1 = 0.5

Функция F(R1) – нормированное значение амплитуды поля в раскрыве параболоидного зеркала, рассчитывается по формуле:

При Y = 2/22 = 11

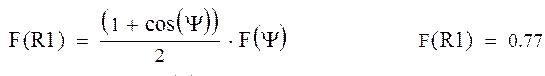
Подставим данные в систему и решим

Расчетные данные заносим в таблицу 4, по которой строим диаграмму направленности зеркала антенны. Затем по данным этой таблицы строим диаграмму направленности антенны.

Таблица 4.

Q	1	2	3	4	5	6	7	8	9	10
U	0.704	1.409	2.112	2.815	3.517	4.218	4.918	5.617	6.313	7.01
L1	0.879	0.562	0.159	-0.191	-0.383	-0.374	-0.204	0.0326	0.227	0.3
L2	0.939	0.772	0.537	0.287	0.074	-0.068	-0.129	-0.119	-0.065	0
L3	0.95	0.85	0.63	0.375	0.27	0.125	0.012	-0.002	-0.003	-0.004
F(Q)	0.909	0.677	0.358	0.053	-0.129	-0.193	-0.144	-0.0212	0.096	0.154

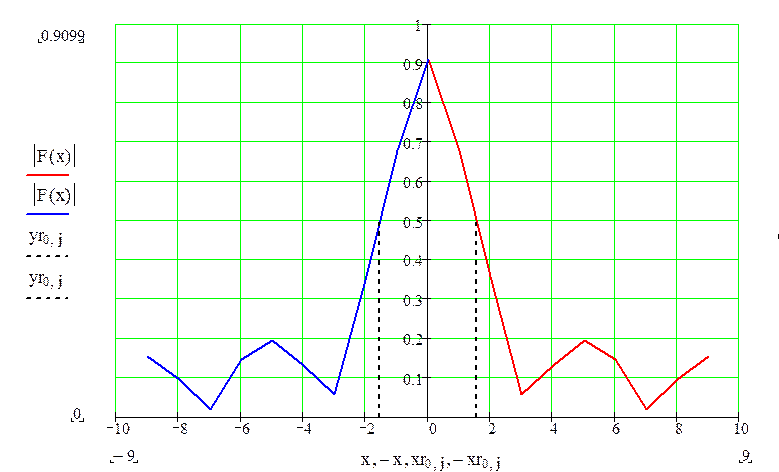
Рис. 9 Диаграмма направленности антенны

Рис. 10 Диаграмма направленности антенны рассчитанная в дБ.

По рассчитанной ДН антенны определяются ширина главного лепестка 2Q0,5 = 3,08.

Уровень первого бокового лепестка в дБ

F(Q)дБ = 10lg(F(Q1) = -6.9897дБ

Список используемой литературы

1.  Конспект лекций по РРВ и АФУ

2.  Задание на курсовой проект и методические указания по его выполнению. М. 1991г.

3.  Методические указания по выполнению курсового проекта. Составитель ст. преподаватель Микрюков М.И.  г. Хабаровск  1995г.

4.  Айзенберг Г.З., Ямпольский Б.Г., Терешин О.Н. Антенны УКВ, М. «Связь», 1977, в 2-х томах.

5.  Кочержевский Г.Н. Антенно-фидерные устройства. М, «Радио-связь» 1981.

6.  Никольский В.В. Антенны, М. «Связь» 1966.