Расчет параболической однозеркальной антенны. Диаграмма направленности пирамидального рупора. Расчет коэффициента направленного действия, страница 2

Bp = Ap · 0.727 = 0.2 · 0.727 = 0.145м

В процессе движения волны в пирамидальном уровне фронт из плоского преобразуется в сферический. Фазовый центр F полученных волн находится в точке пересечения расширяющихся сторон рупора (рис. 2).

 

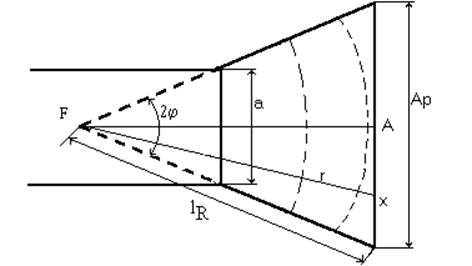
Рис. 2

Поля в раскрыве вследствие изменения формы фронта волны становиться несинфазным, это снижает направленные свойства антенны. Если принять фазу поля в центре раскрыва за нуль. То в точке х фаза поля будет равна:

j х = 3.14x² / l R = 3.14·0.1² / 0.075·0.45 = 0.93м

Где     х = Ар/2 = 0,2/2 = 0,1

Коэффициент бегущей волны КБВ на центральной частоте рассчитываем по формулам:

КБВ = (1-|P|) / (1+|P|)

|P| = (1-l/lв) / (1-l/lв)

|P| = (1-0.075/0.763)/( (1+0.075/0.763)) = 0.0086

КБВ = (1-|0.0086|) / (1+|0.0086|) = 0.983

Рассчитываем КБВ на крайних частотах:

f н = 3,84ГГц и fв = 4,16ГГц

lв  = С / f = 3·10³ / 4,16·10⁹ = 0.072м

lн  = С / f = 3·10³ / 3,84·10⁹ = 0,078м

КБВв = (1-|Pв|) / (1+|Pв|) = (1-|0,0069|) / ((1+|0,0069|) = 0,986

|Pв| = (1-l/lвв) / (1+l/lвв) = (1-0,072/0,073) / (1+0,072/0,073) = 0,0069

 

0,073м 

КБВн = (1-|Pн|) / (1+|Pн|) = (1-0,025) / (1+0,025) = 0,951

|Pн| = (1-lн/lнн) / (1+lн/lнн) = (1-0,078/0,082) / (1+0,078/0,082) = 0,025

 

0,82м

3.  Диаграмма направленности пирамидального рупора

При расчете ДН рупора исходят из того, что амплитудное распределение в раскрыве рупора принимается таким же, как в питающем его волноводе с волной Н10. Это означает, что в плоскости вектора «Н» закон косинуса, в плоскости вектора «Е» амплитуда остается неизменной. При этом считается поле в раскрыве синфазно. В этом случае ДН в плоскости вектора «Е» считается по формуле:

В таблицу 1 заносим рассчитанные данные и по ним строим диаграмму направленности (рис.3).

Таблица 1

Q	0	10	20	30	40	50	60	70	80	90
	1	0.8157	0.4169	0.02517	-0.1559	-0.1761	-0.121	-0.06306	-0.02933	-0.01712
Q	100		110	120	130	140	150	160	170	180
	-0.02059		-0.03157	-0.04069	-0.03836	-0.0206	0.002537	0.0127	0.005984	0

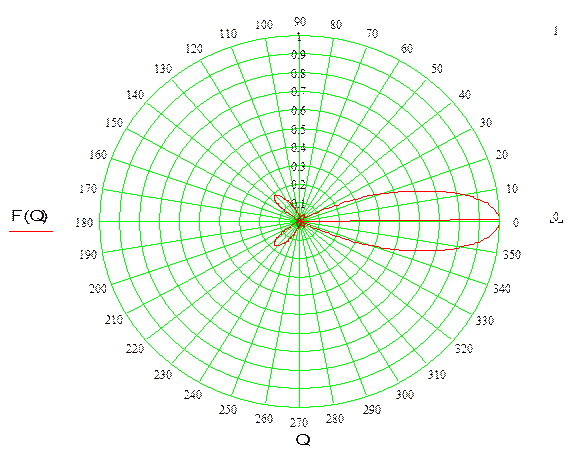
Рис. 3 Диаграмма направленности рупора в плоскости «Е»

Рис. 4 Увеличенный масштаб рисунка 3.

В плоскости «Н» диаграмма направленности имеет вид:

В таблицу 2 заносим рассчитанные данные и по ним строим диаграмму направленности (рис.5).

Таблица 2.

Н	0	10	20	30	40	50	60	70	80	90
	1	0.89015	0.62348	0.33264	0.12398	0.0059997	-0.03848	-0.04610	-0.041556	-0.03506
Н	100		110	120	130	140	150	160	170	180
	-0.029176		-0.02249	-0.012453	0.001307	0.016389	0.024355	0.019318	0.0069234	0

Рис. 5 Диаграмма направленности рупора в плоскости «Н»

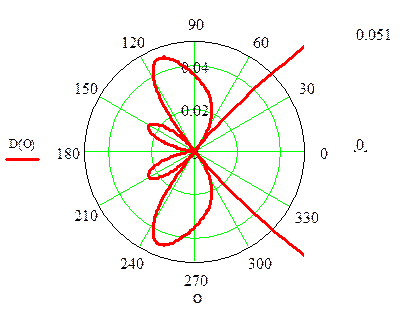
Рис. 6 Боковые лепестки в плоскости «Н»

4.  Расчет геометрических размеров антенны.

4.1 Расчет коэффициента направленного действия

Коэффициент усиления передающей антенны рассчитывается по формуле:

Gпер дБ = 32,28 + 20lg rкм+20lg fМГц–Gпр дБ – (Рпер + |Pпр| - hпер  - hпр)дБ+LдопдБ

Где   Lдоп = 2дБ – затухание в атмосфере

hпер  и hпр – потеря в фидерном тракте, принимаются по 1дБ.

Рпер = 10lg P = 10lg 48 = 16.812дБ

Gпер =

 

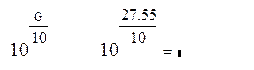Gпер=                                        568.85

Используя связь КУ и КНД и принимая коэффициент полезного действия антенны КПД = 0,85 рассчитываем КНД.

КУ = КПД * КНД

G = КПД * D отсюда D = Gпер / КПД = 568,85/0,85 = 669,24

4.2 Расчет геометрических размеров зеркала.

Радиус раскрыва зеркала определяется из соотношения (рис. 7)

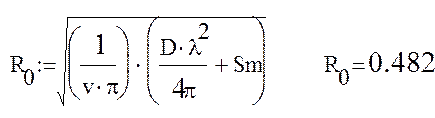
Где    Sm = 0.065 м.кв. – площадь теневой поверхности

V – суммарный коэффициент использования поверхности, 0,4 – 0,6

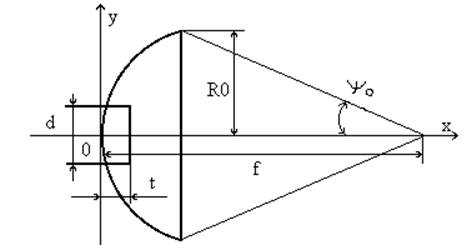
Рис. 7

По диаграмме направленности облучателя определяется оптимальная угловая апертура, которая отсчитывается на уровне 10% мощности излучения от максимума (0,316 по напряженности поля). Такой уровень поля на краю зеркала обеспечивает достаточно низкий уровень боковых лепестков.