




















Лист задания
Начальные
условия: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
Постановка задачи:
1. Рассчитать погрешности уточненных значений.
1.1. Рассчитать уравнения с шагом h.
1.2. Рассчитать уравнения с шагом h/2.
1.3. Оценить погрешности вычислений при решении задачи.
1.4. Рассчитать уточненные решения yут.
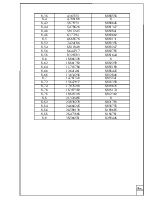
1.5. Составить таблицу данных 1.
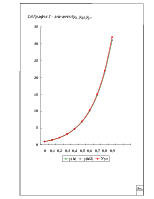
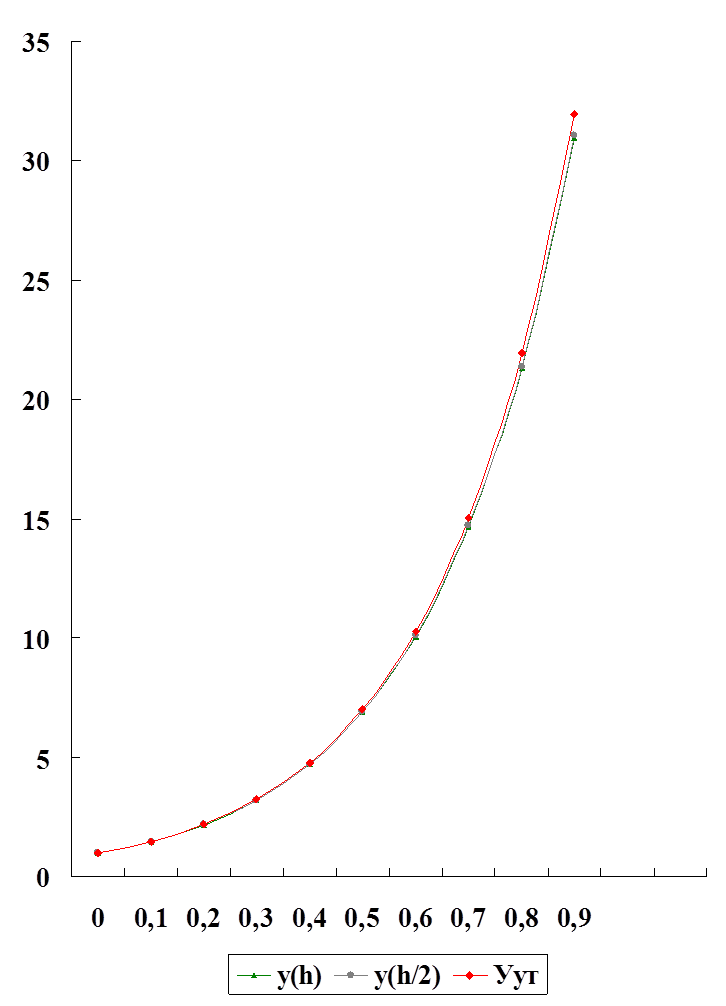
1.6. Построить график 1 – значений yh, yh/2, yут.
2. Аппроксимирование квадратного трехчлена линейным методом.
2.1. Составить таблицу 2 – рассчитанных значений для расчета коэффициентов.
2.2. Составить систему уравнений.
2.3. Решить систему уравнений методом Гаусса.
2.4. Составить таблицу 3 – данных для расчета погрешности аппроксимации.
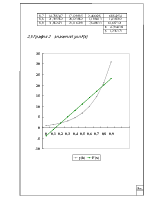
2.5. Построить график 2 – значений yh и F(x).
3. Интерполирование.
3.1. Построить интерполяционный многочлен Лагранжа и сгустить значения.
3.2. Рассчитать погрешность интерполяции.
3.3. Составить таблицу данных 4.
3.4. Построить график 3 – значений y(x), F(x), P(x).
4. Проанализировать полученные результаты
5. Составить программу для проверки правильности расчетов
Содержание
Введение. 4
1.... Расчет погрешностей и уточненных значений.. 4
1.1 Расчет уравнений с шагом h. 4
1.2 Расчет уравнений с шагом h/2. 6
1.3 Оценка погрешности вычислений при решении задачи. 7
1.4 Расчет уточненных решений yут 8
1.5 Таблица данных 1. 9
1.6 График 1 - значений yh, yh/2, yут 11
2. Аппроксимирование квадратного трехчлена методом наименьших квадратов. 12
2.1 Таблица 2 - рассчитанных значений для расчета коэффициентов. 12
2.2 Составление системы уравнений. 12
2.3 Решение системы уравнений методом Гаусса. 13
2.4 Таблица 3 - данных для расчета погрешности. 14
аппроксимации “ξапп”. 14
2.5 График 2 – значений yh и F(x) 15
3. Интерполяция. 16
3.1 Построение интерполяционного многочлена Ньютона. 16
и сгущение значений. 16
3.2 Расчет погрешности интерполяции. 18
3.3 Таблица данных 4. 20
3.4 График 3 - значений y(х), F(X) и P(x) 22
4. Анализ полученных результатов. 23
Заключение. 24
Настоящее время характеризуется резким расширением математики, что связано с созданием и развитием средств вычислительной техники. В результате появления ЭВМ с программным управлением, менее чем за 50 лет скорость выполнения операций возросла от 0,1 операции в секунду при ручном счете до 1012 операций на современных серийных ЭВМ.
Мнение о всемогуществе современных ЭВМ порождает впечатление, разработка численных методов не столь важна. В действительности же, расширение возможностей приложения математики обусловило математизацию химии, экономики, биологии, географии, геологии и д.р. суть математизации состоит в построении новых математических моделей явлений и процессов, а также разработке методов их исследования.
Начальные условия: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
метод Эйлера-Коши, аппроксимирование методом квадратного трехчлена, составление многочлена Лагранжа.
Необходимо вычислить табличные значения решений квадратного уравнения,
используя формулы: ![]() ;
; ![]() ;
;
![]() ;
; 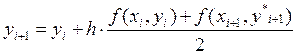
1. х1 = 0,1
![]()
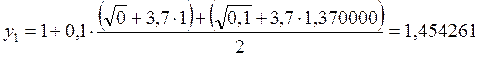
2. х2 = 0,2
![]()
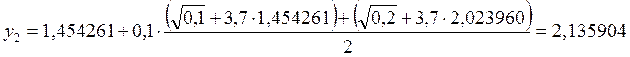
3. х3 = 0,3
![]()
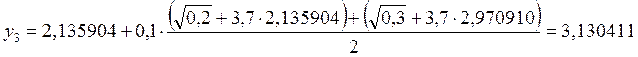
4. х4 = 0,4
![]()
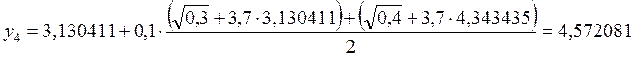
5. х5 = 0,5
![]()
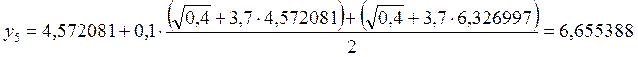
6. х6= 0,6
![]()
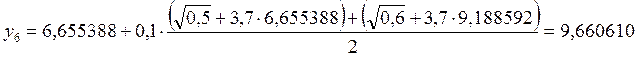
7. х7 = 0,7
![]()
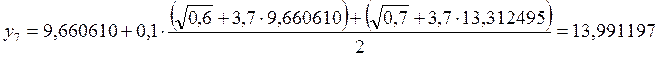
8. х8 = 0,8
![]()
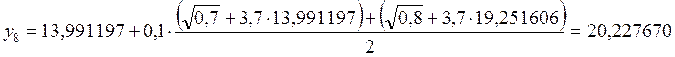
9. х9 = 0,9
![]()
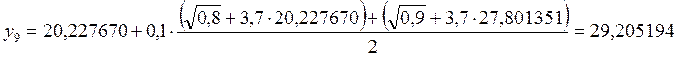
1. х1 = 0,1
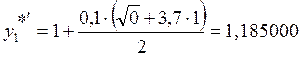
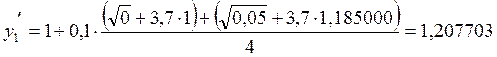
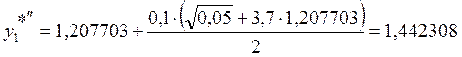
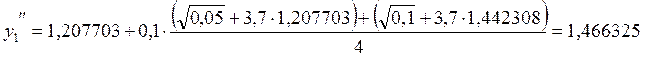
2. х2 = 0,2
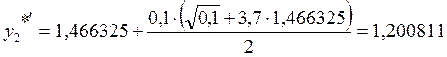
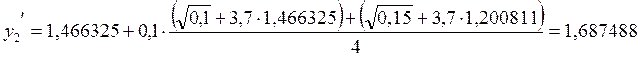
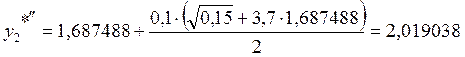
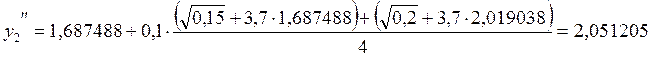
.
.
.
5. х5 = 0,5
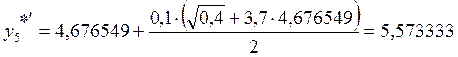
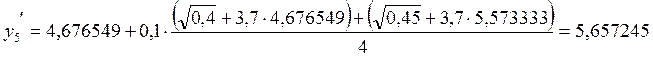
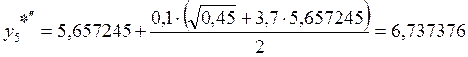
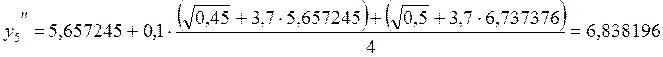
.
.
.
9. х9 = 0,9
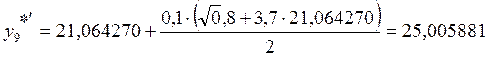
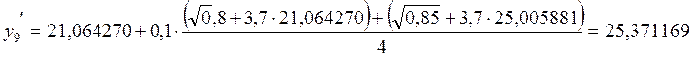
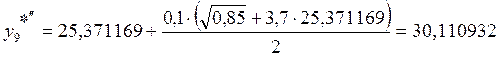
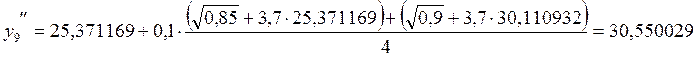
Допустимая погрешность на шаге определяется его максимальной величиной. Шаг интегрирования должен быть таким, чтобы быть существенно меньше интеграла, на котором решение дифференциального уравнения значительно изменяется. Удобный способ оценки погрешности и правильного выбора шага дает метод Рунге.
Погрешность для метода второго порядка точности можно вычислить по следующей формуле:
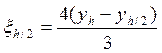
В результате расчетов пришлось уменьшить шаг до ![]() ,
чтобы выполнить условие вычисления погрешности.
,
чтобы выполнить условие вычисления погрешности.
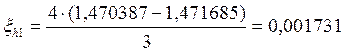
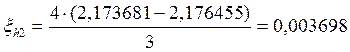
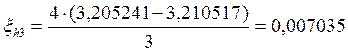
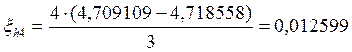
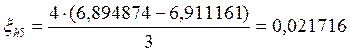
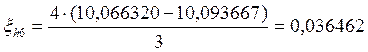
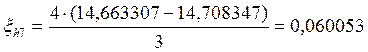
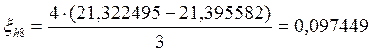
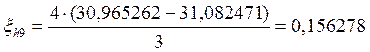
Если ξh/2 по модулю не больше допустимой погрешности, то шаг выбран правильно и находятся уточненные решения:
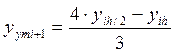
В противном случае шаг уменьшается вдвое и все повторяется.
1. х1 = 0,1
![]()
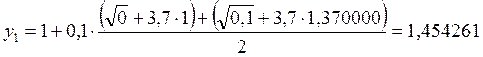
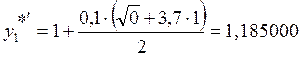
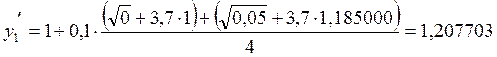
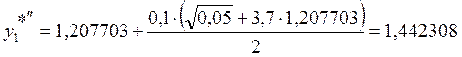
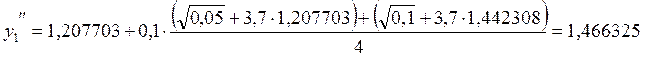
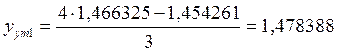
2. х2 = 0,2
![]()
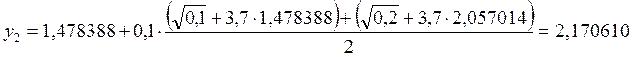
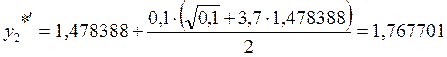
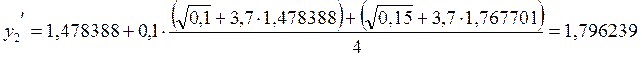
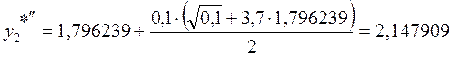
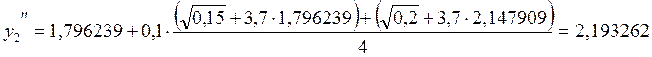
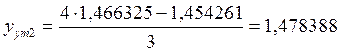
.
.
.
9. х9 = 0,9
![]()
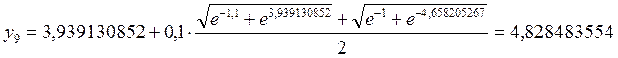
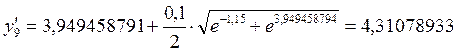
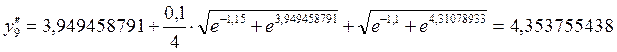
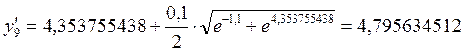
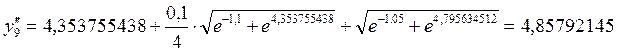
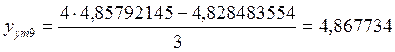 .
.
|
|
|
|
ξhi |
|
|
0,100000 |
1,470387 |
1,471685 |
0,001731 |
1,478388 |
|
0,200000 |
2,173681 |
2,176455 |
0,003698 |
2,193262 |
|
0,300000 |
3,205241 |
3,210517 |
0,007035 |
3,244853 |
|
0,400000 |
4,709109 |
4,718558 |
0,012599 |
4,782654 |
|
0,500000 |
6,894874 |
6,911161 |
0,021716 |
7,024763 |
|
0,600000 |
10,066320 |
10,093667 |
0,036462 |
10,288284 |
|
0,700000 |
14,663307 |
14,708347 |
0,060053 |
15,033829 |
|
0,800000 |
21,322495 |
21,395582 |
0,097449 |
21,930238 |
|
0,900000 |
30,965262 |
31,082471 |
0,156278 |
31,948581 |
|
|
|
|
|
|
|
0,000000 |
1,000000 |
0 |
0,000000 |
|
|
0,100000 |
1,471685 |
0,1180965 |
0,010000 |
|
|
0,200000 |
2,176455 |
0,2759441 |
0,040000 |
|
|
0,300000 |
3,210517 |
0,4800156 |
0,090000 |
|
|
0,400000 |
4,718558 |
0,7388427 |
0,160000 |
|
|
0,500000 |
6,911161 |
1,0640695 |
0,250000 |
|
|
0,600000 |
10,093667 |
1,4723116 |
0,360000 |
|
|
0,700000 |
14,708347 |
1,9887026 |
0,490000 |
|
|
0,800000 |
21,395582 |
2,6544217 |
0,640000 |
|
|
0,900000 |
31,082471 |
3,5452178 |
0,810000 |
|
|
Σ |
4,500000 |
96,470676 |
68,105267 |
2,850000 |
Сумма квадрата разности соответствует значению функции ƒ(x) и F(x):
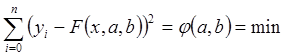
Данная функция – сумма двух переменных (a, b), задача сводится к отысканию ее минимума. Функция двух переменных имеет минимум, когда все ее частные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.