Расчет рекурсивного цифрового фильтра. Методы численного интегрирования. Метод инвариантности импульсной характеристики

МИНИСТЕРСТВО  ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И СВЯЗИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

ХАБАРОВСКИЙ ИНСТИТУТ ИНФОКОММУНИКАЦИИ

(ФИЛИАЛ) ГОУ ВПО СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ

КУРСОВАЯ РАБОТА

по математическим основам цифровой обработки

 сигналов

Тема: Расчет рекурсивного цифрового фильтра

Специальность                                                                       210405

Радиосвязь, радиовещание и телевидение

Вариант                                                                                  № 30

Выполнил                                                                                       

Руководитель проекта                                                                    

Зав. Отделением                                                                                

Хабаровск

2011

СОДЕРЖАНИЕ

	Техническое задание	3
	Исходные данные на вариант № 30	4
	Введение	5
1	Графическое представление задачи	6
1.1	Методы проектирования рекурсивных цифровых фильтров	7
1.2	Методы численного интегрирования	8
1.3	Метод инвариантности импульсной характеристики	10
1.4	Метод билинейного преобразования	12
1.5	Обобщенное биноминальное преобразование	13
2.	Расчет передаточной функции аналогового фильра и преобразование ее в передаточную функцию цифрового фильтра	14
3.	Структурная схема цифрового  фильтра	22
4.	Методы реализации цифрового фильтра	23
4.1	Аппаратный метод	23
4.2	Программный метод	24
4.3	Аппаратно-программный метод	25
	Заключение	27
	Список используемой литературы	28

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

По исходным данным необходимо выполнить расчет рекурсивного цифрового фильтра.

Считаются заданными следующие параметры:

1 Вид фильтра: ФНЧ, ФВЧ.

2 Тип фильтра: Баттерворта (Б) или Чебышева (Ч).

3 Частота дискретизации  fд.

4 Границы полос пропускания (ПП) :

-верхняя граница полосы пропускания  fп   для ФНЧ;

-нижняя граница  полосы пропускания  fп   для ФВЧ;

5 Границы полос задерживания (ПЗ);

-нижняя граница ПЗ  fз  для ФНЧ;

-верхняя граница ПЗ  fз  для ФВЧ.

6 Допустимая неравномерность амплитудно-частотной  характеристики в ПП   ∆A max, дБ.

7 Минимально допустимое ослабление в ПЗ А min, дБ.

ИСХОДНЫЕ ДАННЫЕ НА ВАРИАНТ № 30

Вид фильтра ФНЧ

Тип фильтра Баттерворта

Частота дискретизации fд = 16 кГц

Границы полос пропускания fп = 1.7 кГц

Границы полос задерживания fз = 3.8 кГц

Допустимая неравномерность ПП ∆A max = 1.35 дБ

Допустимое ослабление ПЗ А min = 25 дБ.

Преподаватель_____________         Студент___ ____________

“__27__”  _______мая_______ 2011 г.

ВВЕДЕНИЕ

Высококачественные частотные нерекурсивные цифровые фильтры (НЦФ) имеют, как правило, большую ширину окна (многочленный оператор фильтра). Чем меньше допустимая ширина переходной зоны частотной характеристики фильтра между полосами пропускания и подавления, тем больше окно фильтра. Альтернативное решение - применение рекурсивных цифровых фильтров (РЦФ), для которых количество коэффициентов фильтра может быть сокращено на несколько порядков по сравнению с НЦФ.

Рекурсивные фильтры имеют определенную "память" по значениям предыдущих отсчетов, которая, в пределе, может быть бесконечной. С учетом этого фактора рекурсивные фильтры получили название фильтров с бесконечной импульсной характеристикой (БИХ-фильтров), в отличие от нерекурсивных фильтров, всегда имеющих конечную импульсную характеристику (КИХ-фильтры). Реакция рекурсивного фильтра на сигнал с учетом "памяти" исключает возможность создания фильтров с четным импульсным откликом, и частотные характеристики рекурсивных фильтров всегда являются комплексными. Проектирование рекурсивных частотных фильтров с заданными частотными характеристиками осуществляется с использованием z-преобразований.

1.  Графическое представление задачи

Отобразим графически требования к АЧХ фильтра нижних частот, для этого потребуется вычислить:

                  

             

              

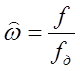
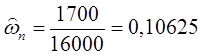
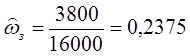
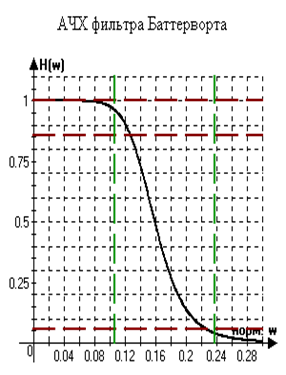
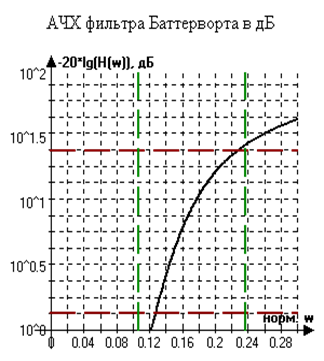
Рисунок 1 – АЧХ фильтра Баттерворта и АЧХ фильтра

Баттерворта в Дб.

1.1.  Методы проектирования рекурсивных цифровых фильтров

Передаточная функция цифровых БИХ-фильтров задаются соотношением 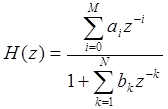, которая подобна передаточной функции АФ при замене переменной z на s. Следовательно, одним из подходов к проектированию цифровых БИХ-фильтров является преобразование передаточной функции АФ в передаточную функцию ЦФ. Чтобы ЦФ обладали требуемыми свойствами как их АФ, требуется выполнения двух условий:

1.  Мнимая ось s-плоскости () отображалась в единичную окружность в z-плоскости (). Это условие необходимо для сохранения частотных характеристик АФ.

2.  Левая половина s-плоскости () отображалась в z-плоскости внутри единичного круга (). Это условие необходимо для сохранения свойств устойчивости АФ.

1.2.  Метод численного интегрирования

Дифференциальное уравнение, описывающее АФ заменяется на разностное уравнение ЦФ, путем аппроксимации производной некоторыми конечными разностями. Эта операция приводит к замене комплексной переменной s в передаточной функции АФ на комплексную переменную z в передаточной функции ЦФ.

Различные методы численного интегрирования дадут различные функции перехода и, следовательно, различные результирующие ЦФ. Рассмотрим метод Эйлера, аппроксимирующий производную по времени непрерывной функции  конечной разностью вида

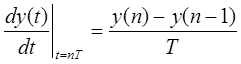, где T – интервал дискретизации, а y(n)=y(nT). В операторной форме уравнение дает

.

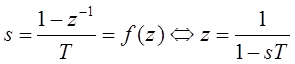Покажем, что данный метод удовлетворяет двум выше указанным условиям:

1. 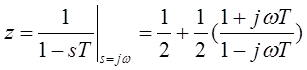  или 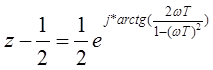 из этого следует что  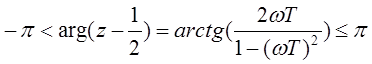при .

2.  При  тогда 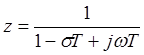 и, следовательно, .

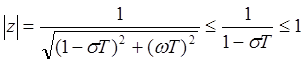1.3.  Метод инвариантности импульсной характеристики

Импульсная характеристика h(n) результирующего ЦФ представляет собой выборки импульсной характеристики h(t) соответствующего АФ.

, где T – интервал дискретизации

Рассмотрим передаточную функцию H(s) исходного АФ

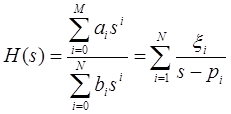, где и все полюсы различны,  представляет собой i-й полюс АФ,  вычет H(s) в полюсе . Импульсную характеристику h(t) АФ можно получить, осуществив обратное преобразование Лапласа

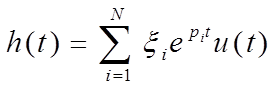, где u(t) - единичная ступенчатая последовательность. Тогда импульсная характеристика h(n) ЦФ

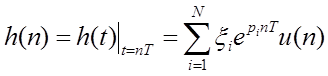, где u(n) - единичная ступенчатая последовательность. Передаточная функция H(z) результирующего ЦФ определяется путем нахождения z-преобразования импульсной характеристики

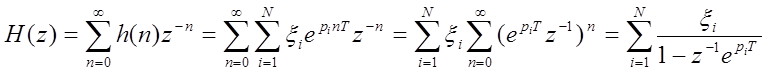
Сравнивая H(s) и H(z), получаем соотношения перехода от аналоговых фильтров к цифровым фильтрам

.

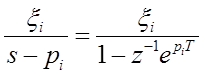Данный метод применим только к ФНЧ и ФПЧ, так как обладает эффектом наложения спектров из-за неоднозначной функции перехода из s-плоскости в z-плоскости.

:

1.4.  Метод билинейного преобразования

Данный метод определяет однозначную функцию перехода из s-плоскости в z-плоскости, но имеет искажение частотной характеристики и не сохраняет импульсной характеристики. Искажение частотной характеристики ЦФ может быть компенсировано