

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЦФ
Важнейшей характеристикой ЦФ в частотной области является системная (передаточная) функция H(z), которая (по определению) является z-преобразованием импульсной функции g(k) этого фильтра, т. е.
H![]() .
(8)
.
(8)
k=0
Откуда импульсная функция ЦФ
![]() g(k) = 2π1jz
g(k) = 2π1jz∫=H1
(z) zk−1dz.
(9)
Интеграл в выражении (9) берётся по любому замкнутому контуру в области сходимости (области устойчивой работы ЦФ), охватывающему начало координат z-плоскости [4, с. 274]. Поэтому контур интегрирования можно свести к окружности единичного радиуса. При таком интегрировании имеет место равенство z = e jω∆t .
Подставив в выражения (5) и (2) z = e jω∆t , переходят от системных функций H(z) к комплексным передаточным функциям (или комплексным коэффициентам передачи) нерекурсивного и рекурсивного фильтров:
jω∆t ) = N∑−1ane−jnω∆t =a0 +a1e−jω∆t +...+aN−1e−j(N−1)ω∆t ;
![]()
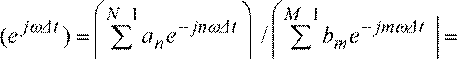 H
(10) (e n
H
(10) (e n
−
H
![]() +
b1e −jωn∆=t0+
a2e−
j2ω∆t +...m=+0aN−1e−
j(N−!)ω∆t , при b0 =1. (11)
+
b1e −jωn∆=t0+
a2e−
j2ω∆t +...m=+0aN−1e−
j(N−!)ω∆t , при b0 =1. (11)
= a10 + a1e− jω∆t + b1e− j2ω∆t + ... + bM −1e− j(M−1)ω∆t
Комплексные передаточные функции получают, подавая на вход ЦФ последовательность х(k) =e jωk∆t , которая функционально эквивалентна дискретной синусоиды с частотой ω, где ω∆t∈ (0; 2π).
Итак, на окружности единичного радиуса ( z = e jω∆t ) выражение (8) переходит в
H![]() , (12) k=0
, (12) k=0
где H(ω∆t)
=![]() H(e
jω∆t)
H(e
jω∆t)![]() - модуль
комплексной передаточной функции, называемый амплитудно-частотной
характеристикой (АЧХ) фильтра, определяющий амплитуду выходного сигнала
фильтра в установившемся режиме при входном сигнале х(k) = e jωk ∆t ; Ψ(ω∆t)
- аргумент комплексной частотной характеристики, называемый фазо-частотной
характеристикой (ФЧХ) цифрового фильтра, определяющий фазу выходного сигнала
устойчивого фильтра при входном сигнале х(k) = e jωk∆t .
- модуль
комплексной передаточной функции, называемый амплитудно-частотной
характеристикой (АЧХ) фильтра, определяющий амплитуду выходного сигнала
фильтра в установившемся режиме при входном сигнале х(k) = e jωk ∆t ; Ψ(ω∆t)
- аргумент комплексной частотной характеристики, называемый фазо-частотной
характеристикой (ФЧХ) цифрового фильтра, определяющий фазу выходного сигнала
устойчивого фильтра при входном сигнале х(k) = e jωk∆t .
Соотношение (12) показывает, что частотные характеристики АЧХ и ФЧХ) цифровых фильтров являются непрерывными функциями частоты ω и определяются всего лишь весовыми коэффициентами в прямых an и обратных bm (для рекурсивных фильтров) связях и шагом дискретизации ∆t.
Важнейшим свойством частотных характеристик ЦФ является то, что они представляют собой периодические функции угловой частоты ωс периодом, равным частоте дискретизации ωд = 2π/ ∆t = 2πfд (в рад/c), т. к. e jωk∆t =e j(ω+mωд)k∆t , где m - целое.
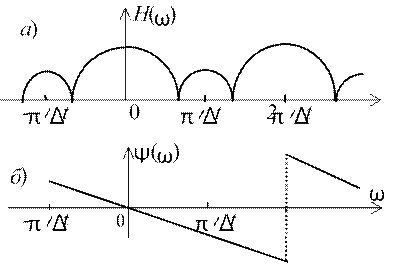
Для фильтров, системные функции которых имеют только вещественные коэффициенты an иbm, АЧХ H(ω∆t) представляет собой чётную функцию частоты, а ФЧХ Ψ(ω∆t) - нечётную функцию частоты на интервале -π/∆t < ω < π/∆t (рис. 6). Для построения АЧХ фильтра в диапазоне от 0 до ω = ωд = 2π/ ∆t следует вычислить модуль выражения
 (12) при изменении угла ω∆t
от 0 ω
до 2π,
т. е. при одном обходе окружности единичного радиуса на z-плоскости [4, с.
274]. При последующих обходах окружности АЧХ периодически повторяется.
(12) при изменении угла ω∆t
от 0 ω
до 2π,
т. е. при одном обходе окружности единичного радиуса на z-плоскости [4, с.
274]. При последующих обходах окружности АЧХ периодически повторяется.
Из этих свойств АЧХ следует, что практически она имеет
Рис. 6 смысл лишь в интервале частот от 0 до ω = π/∆t и требования к
частотным характеристикам ЦФ достаточно задавать лишь на интервале угловых частот [0; π/∆t]. На верхней частоте этого интервала каждому периоду дискретизированного гармонического сигнала соответствует два отсчёта. По теореме Котельникова это есть предельное значение частоты сигнала, который может быть однозначно восстановлен по своим отсчётам.
Для сравнения частотных характеристик различных ЦФ угловую частоту ω нормируют: её задают в долях от дискретной угловой частоты ωд, т. е. при ∆t = 1, ω€ =ω/ωд = 2πw, где w =ω€/ 2π- относительная циклическая частота ЦФ. Тогда требования к частотным характеристикам ЦФ следует задавать на интервале w = [0…0,5]. При этом изменяются аргументы в обозначениях частотных характеристик: H(e j2πw), H(w), Ψ(w).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.