


















Скалярное поле, производная по направлению, градиент
Определение. Скалярным полем называется часть пространства, каждой точке которой отнесено значение некоторой скалярной величины.
Скалярным полем, например, является поле атмосферного давления.
Пусть нам задано
скалярное поле функции ![]() в
некоторой области
в
некоторой области ![]() .
Рассмотрим в поле некоторую точку
.
Рассмотрим в поле некоторую точку ![]() и
выберем направление, единичный вектор направления (рисунок 4.1):
и
выберем направление, единичный вектор направления (рисунок 4.1):
![]()

Рисунок 4.1
Возьмем на
направлении этого вектора точку ![]() .
Расстояние между
.
Расстояние между ![]() и
и
![]() обозначим
обозначим
![]() .
.
Приращение
функции ![]() при
переходе от точки
при
переходе от точки ![]() в
точку
в
точку ![]() обозначим:
обозначим:
![]()
Определение.
Производной функции ![]() по
направлению
по
направлению ![]() в точке
в точке ![]() называется
предел отношения приращения функции
называется
предел отношения приращения функции ![]() к
к ![]() при
при ![]() :
:
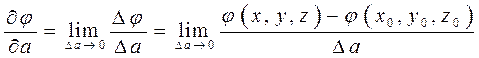
Вычисляется производная по направлению по формуле:
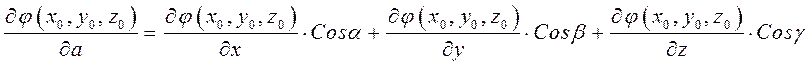
Производная по
направлению определяет скорость изменения функции ![]() в точке
в точке ![]() в
направлении
в
направлении ![]() .
.
Если скалярное поле плоское, то:
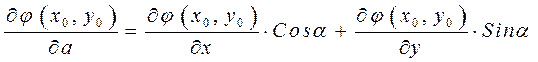
Определение.
Градиентом поля ![]() в
точке
в
точке ![]() называется
вектор, координаты которого равны значениям частных производных функции
называется
вектор, координаты которого равны значениям частных производных функции ![]() в точке
в точке ![]() .
.
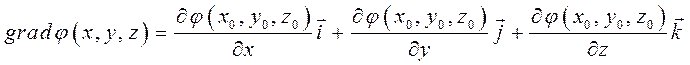
Можно доказать,
что  .
.
Так как скалярное
произведение ![]() ,
,
![]() , то
, то ![]() , то есть
, то есть
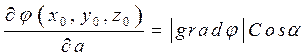 .
.
Из последнего соотношения следует,
что производная по направлению принимает наибольшее значение, если ![]() , то есть
направление
, то есть
направление ![]() совпадает
с направлением градиента и это наибольшее значение равно модулю градиента.
совпадает
с направлением градиента и это наибольшее значение равно модулю градиента.
Пример. Дана
функция ![]() и точка
и точка ![]() . Найти
. Найти ![]() и
производную
и
производную ![]() в точке
в точке ![]() по
направлению к точке
по
направлению к точке ![]() .
.
Решение. Найдем
значения частных производных функции ![]() в точке
в точке ![]() :
:
 ;
; 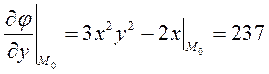 ;
; 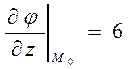 .
.
![]()
направление  ;
;
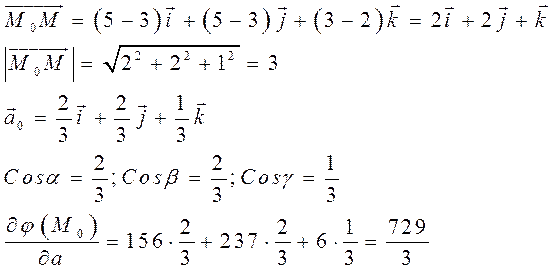
Векторное поле, поток вектора
Определение. Векторным полем называется часть пространства, в каждой точке которого задана некоторая векторная величина.
Если эта векторная величина сила, то мы имеем силовое поле. Если рассмотреть текущую жидкость, скорость частиц жидкости – векторная величина, мы получаем поле скоростей текущей жидкости и т.д.
Векторное поле
задано, если в каждой точке поля ![]() указан
соответствующий этой точке вектор
указан
соответствующий этой точке вектор ![]() .
.
Мы будем
рассматривать стационарные поля, в которых вектор ![]() зависит
только от точки
зависит
только от точки ![]() и
не зависит от времени. Обозначим координаты вектора
и
не зависит от времени. Обозначим координаты вектора ![]() :
: ![]() . Тогда:
. Тогда:
![]()
Рассмотрим в
векторном поле поверхность ![]() и
выберем на ней определенную сторону. Здесь рассматриваются только двухсторонние
поверхности. Обозначим через
и
выберем на ней определенную сторону. Здесь рассматриваются только двухсторонние
поверхности. Обозначим через ![]() единичный
вектор нормали к выбранной стороне поверхности в произвольной ее точке.
Проекции вектора
единичный
вектор нормали к выбранной стороне поверхности в произвольной ее точке.
Проекции вектора ![]() .
.
Определение.
Потоком вектора ![]() через
поверхность
через
поверхность ![]() называется
интеграл по поверхности
называется
интеграл по поверхности ![]() от
скалярного произведения вектора поля
от
скалярного произведения вектора поля ![]() на
единичный вектор нормали
на
единичный вектор нормали ![]() :
:
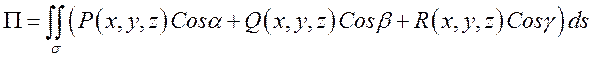 (4.1)
(4.1)
Если ![]() - поле
скоростей текущей жидкости, то данный интеграл выражает поток жидкости через
поверхность
- поле
скоростей текущей жидкости, то данный интеграл выражает поток жидкости через
поверхность ![]() .
Интеграл (4.1) можно представить в виде:
.
Интеграл (4.1) можно представить в виде:
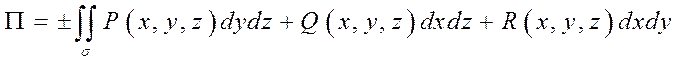 (4.2)
(4.2)
Знак перед интегралом определяется следующим образом: если угол между нормалью к поверхности и осью координат, проекция на которую задана острый, то знак плюс (косинус такого угла положительный); если угол тупой, то знак минус (в этом случае косинус отрицательный).
Для вычисления интеграла мы рассматриваем интегралы от каждого слагаемого отдельно и выражаем под интегральное выражение через две переменные, стоящие под знаками дифференциалов. Тем самым мы переходим от поверхностных интегралов к двойным.
Пример.
Найти поток поля вектора ![]() через
часть плоскости
через
часть плоскости ![]() ,
вырезанную координатными плоскостями.
,
вырезанную координатными плоскостями.
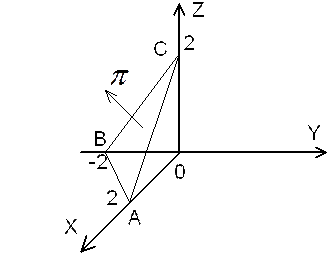
Решение. Проекции вектора поля на оси OX и OY равны:
![]()
По формуле (4.2) имеем:
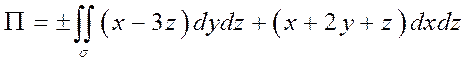
![]() -
треугольник АВС.
-
треугольник АВС.
Рассмотрим 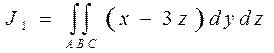 .
.
Подынтегральная функция – проекция
вектора ![]() на ось OX. Угол между нормалью к треугольнику АВС и осью ОХ острый, поэтому знак
перед интегралом “+”. Выразим
на ось OX. Угол между нормалью к треугольнику АВС и осью ОХ острый, поэтому знак
перед интегралом “+”. Выразим ![]() через
через ![]() и
и ![]() ,
используя уравнения плоскости:
,
используя уравнения плоскости:
![]()
Тем самым мы спроектируем треугольник АВС на плоскость YOZ. Получим треугольник ВОС, тогда:

Уравнение ВС: ![]()
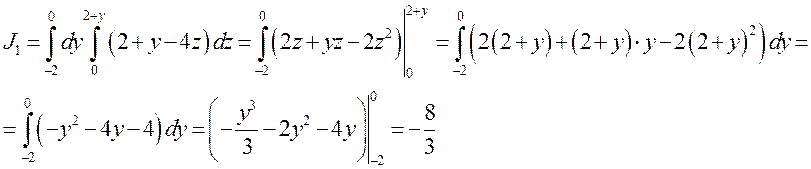
Рассмотрим интеграл от второго
слагаемого ![]() . Функция
. Функция
![]() -
проекция вектора
-
проекция вектора ![]() на
ось OY. Угол между нормалью к треугольнику АВС и осью OY – тупой. Поэтому перед интегралом поставим знак
на
ось OY. Угол между нормалью к треугольнику АВС и осью OY – тупой. Поэтому перед интегралом поставим знак ![]() .
.
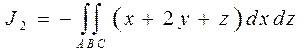
Выразим ![]() через
через ![]() и
и ![]() :
: ![]() . Тем
самым мы спроектируем треугольник АВС на плоскость XOZ,
получим треугольник АОС:
. Тем
самым мы спроектируем треугольник АВС на плоскость XOZ,
получим треугольник АОС:
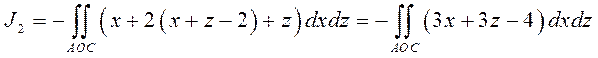
Уравнение АС: ![]() .
.
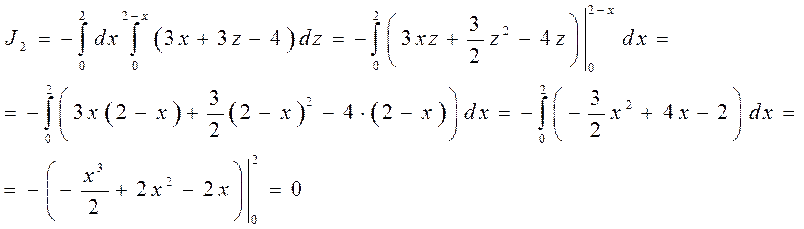
Таким образом, поток вектора ![]() через
треугольник АВС равен:
через
треугольник АВС равен:
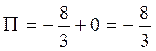
Найдем
поток вектора ![]() через
полную поверхность пирамиды ОАВС. Поток вектора через поверхность пирамиды
равен сумме потоков через грани пирамиды. Мы нашли поток через грань АВС:
через
полную поверхность пирамиды ОАВС. Поток вектора через поверхность пирамиды
равен сумме потоков через грани пирамиды. Мы нашли поток через грань АВС: 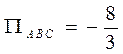 . Найдем
поток вектора
. Найдем
поток вектора ![]() через
грань ВОС:
через
грань ВОС:
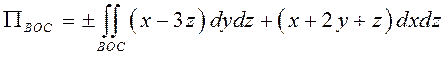
Уравнение
плоскости, на которой лежит треугольник ВОС: ![]() ; тогда
; тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.