Расчет нерекурсивного цифрового фильтра. Основные этапы проектирования нерекурсивных цифровых фильтров

Одним из наиболее часто встречающихся в технике устройством преобразования сигналов является фильтр, расчету которого и посвящена данная работа.

1 Основные этапы проектирования     нерекурсивных цифровых фильтров

Цифровой фильтр (ЦФ) – это линейная дискретная система, которая описывается разностным уравнением

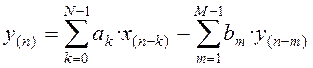                 (1.1)

где  – количество значений входного сигнала в предыдущие моменты времени и в данный момент, которым определяется выходной сигнал;

 – количество значений выходного сигнала в предыдущие моменты времени, которым определяется выходной сигнал в данный момент времени.

Такой фильтр в общем случае называется рекурсивным. Если же все коэффициенты  равны 0, то такой фильтр называется нерекурсиным или трансверсальным, тогда он описывается уравнением

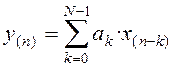                      (1.2)

В любом случае любой ЦФ может быть представлен в виде комбинации сумматоров, линий задержки, умножителей, что является следствием его математического представления формулой (1.1).

Рассмотрим основные этапы проектирования нерекурсивных ЦФ.

Первый этап – формулировка задачи аппроксимации – включает в себя следующие шаги:

-  выбор типа фильтра (с линейной ФЧХ определенного вида или минимально-фазового);

-  выбор аппроксимирующей функции , значения которой определяют требуемую характеристику фильтра, например АЧХ. Здесь ‑ нормированная частота, ‑ вектор коэффициентов, совпадающий с вектором коэффициентов фильтра а или достаточно просто связанный с ним;

-  определение аппроксимируемой функции , задающей требования к заданной характеристике;

-  выбор критерия аппроксимации, т.е. уточнение смысла приближенного равенства   при заданных значениях ;

-  определение весовой функции аппроксимации , задающей требования к точности приближенного равенства (1.6). Целью первого этапа является математическая формулировка задачи вычисления вектора  по заданным требованиям к характеристике фильтра.

Второй этап – решение задачи аппроксимации – включает в себя следующие шаги:

-  оценку необходимого порядка фильтра ;

-  расчет вектора коэффициентов ;

-  проверку критерия получения решения (выполнение заданных требований к характеристикам фильтра).

Если требования к характеристикам выполняются, то по вектору коэффициентов определяется вектор и второй этап заканчивается. Если требования не выполняются, необходимо вернуться ко второму шагу и рассчитать вектор  при большем значении .

Целью второго этапа является определение вектора коэффициентов фильтра .

Третий этап – расчет разрядности  коэффициентов (или разрядности регистров ПЗУ) – зависит от выбранной элементной базы. При реализации фильтра на специализированном микропроцессоре типа DSP значение  задано и на третьем этапе остается проверить, выполняются ли заданные требования к характеристикам фильтра. Если требования выполняются, то следует перейти к четвертому этапу, если нет – то вернуться ко второму этапу, повторить решение аппроксимационной задачи при большем  и снова перейти к третьему этапу. Если фильтр реализуется на БИС общего применения или универсальных микропроцессорах, то необходимо минимизировать значение , уменьшая его до тех пор, пока заданные требования к характеристикам перестанут выполняться.

На четвертом этапе рассчитываются разрядности регистров оперативной памяти таким образом, чтобы мощность собственных шумов фильтра была меньше, чем мощность шума на входе. На пятом этапе осуществляется схемная реализация фильтра на выбранной элементной базе.

2 Классификация цифровых фильтров

Фильтры классифицируют исходя из требований к АЧХ и ФЧХ. Бывают фильтры с линейной ФЧХ и нелинейной. Следует отметить, что у рекурсивных фильтров точно линейная ФЧХ недостижима, а в качестве требования задается минимум группового времени задержки . У нерекурсивных же фильтров достижима точно-линейная ФЧХ. Такие фильтры делятся на четыре группы, в зависимости от вида