Статистическое кодирование. Коэффициент избыточности. Ветвление кодовых комбинаций. Средняя длина кодовой комбинации

7. Статистическое кодирование.

Для дискретных каналов без помех К. Шенноном была доказана следующая теорема: если производительность источника R_И<С-ε, где e - сколь угодно малая величина, то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника. Передачу всех сообщений при R_И>C осуществить невозможно.

Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений. Статическим или оптимальным называется кодирование, при котором пропускная способность канала связи без помех используется наилучшим образом. При оптимальном кодировании фактическая скорость передачи сообщений по каналу R приближается к пропускной способности С, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответствовали ограничениям, которые накладываются на сигналы, передаваемые по каналу связи. Поэтому структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.

Энтропия источника сообщений.

В теории связи основное значение имеет не количество информации, содержащееся в отдельном сообщении, а среднее количество информации, создаваемое источником сообщений. Среднее значение (математическое ожидание) количества информации, приходящееся на одно элементарное сообщение, называется энтропией источника сообщений.

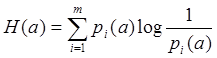
Как видно из формулы, энтропия источника определяется распределением вероятностей выбора элементарных сообщений из общей совокупности. Обычно отмечают, что энтропия характеризует источник с точки зрения неопределенности выбора того или иного сообщения. Энтропия всегда величина вещественная, ограниченная и неотрицательная: H(x)>0.

Найдем энтропию источника сообщений:

m-объем алфавита дискретного источника = 2;

вероятность приема “1” (Р(1)) = 0,8;

вероятность приема “0” (Р(0)) = 0,2;

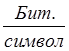Для вычисления энтропии воспользуемся формулой:

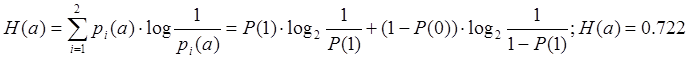При m=2 H_max(a)=1 наблюдается при равновероятном приеме 0 и 1, т.е. P(1)=P(0)=0,5. Если же энтропия не максимальна, то вводят коэффициент избыточности.

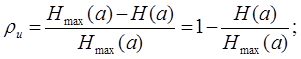
Этот коэффициент показывает, какая доля максимально возможной энтропии не используется источником. Если ρ_и>20%, то необходима перекодировка сообщения для снижения коэффициента избыточности.

Подсчитаем  коэффициент избыточности :

H(a)=0.722;H_max(a)=log₂m=log₂2=1; ,тогда…

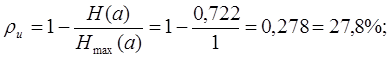
Коэффициент избыточности получился больше 20%, следовательно, необходима перекодировка сообщения.

Для повышения эффективности передачи сообщение должно быть закодировано таким образом, чтобы  коэффициент избыточности (ρ_и) кодовой последовательности был как можно меньше. Коды, обеспечивающие такое преобразование, называют статистическими. Если источник не имеет памяти и избыточность обусловлена только неравновероятностью элементов сообщения, то она может быть уменьшена кодированием наиболее вероятных элементов сообщения в наиболее короткие, а наименее вероятных—в наиболее длинные кодовые комбинации.

Наибольшее снижение избыточности, достигается кодированием по методу Фано-Шеннона-Хаффмена.

Осуществим статистическое кодирование восьми трехбуквенных комбинаций, состоящих из элементов двоичного кода 1 и 0: 000, 001, 010, 011  100, 101, 110, 111. Для кодирования воспользуемся алгоритмом неравномерного кодирования Хаффмена.

Для этого:

1. Вычислим вероятности этих комбинаций и расположим их в порядке убывания вероятностей в таблицу (таблица 7.1).

Таблица 7.1

P(a₁)=P(0)·P(0) ·P(0)=0.2·0.2·0.2=0.008;

P(a₂)=P(0)·P(0) ·P(1)=0.2·0.2·0.8=0.032;

P(a₃)=P(0)·P(1) ·P(0)=0.2·0.8·0.2=0.032;

P(a₄)=P(1)·P(0) ·P(0)=0.8·0.2·0.2=0.032;

P(a₅)=P(1)·P(0) ·P(0)=0.2·0.2·0.2=0.128;

P(a₆)=P(1)·P(0) ·P(1)=0.2·0.2·0.2=0.128;

P(a₇)=P(1)·P(1) ·P(0)=0.2·0.2·0.2=0.128;

P(a₈)=P(1)·P(1) ·P(1)=0.8·0.8·0.8=0.512;

2. Составим сводную таблицу ветвления кодовых комбинаций по принципу:

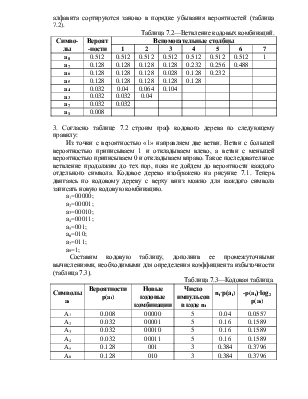
Два последних символа в начальном столбце, с наименьшими вероятностями, объединяют в одну группу и приписывают ей суммарную вероятность объединяемых символов в следующем столбце. Символы алфавита сортируются заново в порядке убывания вероятностей (таблица 7.2).

Таблица 7.2—Ветвление кодовых комбинаций.

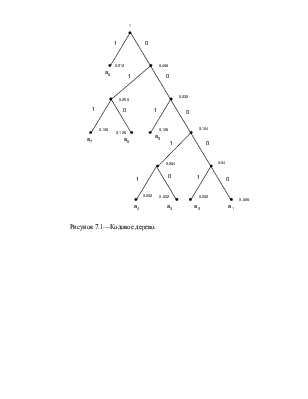
3. Согласно таблице 7.2 строим граф кодового дерева по следующему правилу:

Из точки с вероятностью «1» направляем две ветви. Ветви с большей вероятностью приписываем 1 и откладываем влево, а ветви с меньшей вероятностью приписываем 0 и откладываем вправо. Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждого отдельного символа. Кодовое дерево изображено на рисунке 7.1. Теперь двигаясь по кодовому дереву с верху вниз можно для каждого символа  записать новую кодовую комбинацию.

а₁=00000;

а₂=00001;

а₃=00010;

а₄=00011;

а₅=001;

а₆=010;

а₇=011;

а₈=1;

Составим кодовую таблицу, дополнив ее промежуточными вычислениями, необходимыми для определения коэффициента избыточности (таблица 7.3).

                                                                               Таблица 7.3—Кодовая таблица.

Средняя длина кодовой комбинации вычисляется по формуле: