написании пособия использована следующая литература:
1. Ф.А. Новиков, Дискретная математика для программистов, Питер, 2000
2. С.В. Яблонский, Введение в дискретную математику, Наука, 1986
3. М. Свами, К. Тхуласираман, Графы,сети,алгоритмы, Мир, 1984 4. А. Я. Савельев, Основы информатики, Издательство МГТУ им. Н.Э.Баумана, 2001
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.
Например, множество S страниц этого пособия, множество N натуральных чисел, множество R вещественных чисел, множество A различных символов на этой странице.
Если объект x является элементом множества M, то говорят, что х принадлежит М. Обозначение x∈ M , в противном случае x∉ M .
Множества, как объекты, могут быть элементами других множеств. Множество, не содержащее элементов, называется пустым. Обозначение ∅. Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U ( своего для каждого случая), которое называется универсумом.
Задать множество можно различными способами :
перечислением элементов M := {a1,a2,K,ak }; характеристическим предикатом M := {x | P( )x }; порождающей процедурой M := {x | x := f }.
1) M1 := {1,2,3,4,5,6,7,8,9};
2) M2 := {n | n∈ N & n <10};
3) M3 := {n | FOR n =1 TO 9 : PRINT n : NEXT n}.
Перечислением можно задавать только конечные множества.
Множество А называют подмножеством множества В, если каждый элемент множества А принадлежит множеству В. Обозначение A ⊂ B . Надо заметить, что ∅ есть подмножество любого множества. Из определения также следует, что любое множество является своим подмножеством.
![]() Мощность множества М обозначается как M . Для конечных множеств мощность – это количество
элементов.
Мощность множества М обозначается как M . Для конечных множеств мощность – это количество
элементов.
Обычно рассматриваются следующие операции над множествами: объединение
A∪ B := {x | x∈ A∨ x∈ B} ,где значком ∨ обозначено «или»; пересечение
A∩ B := {x | x∈ A& x∈ B} , где значком & обозначено «и»; разность
AΔB := {x | (x∈ A& x∉ B) ∨ (x∈ B & x∉ A)}; дополнение
![]()
A := {x | x∉ A}, операция подразумевает некоторый универсум
A3 = { }1,5 .
Пусть A = {1,2,3}, B = {3,4,5}, U = {1,2,3,4,5,6}. Тогда
![]()
A∪ B = {1,2,3,4,5}, A∩ B = {3}, A \ B = {1,2}, AΔB = {1,2,4,5}, A = {4,5,6}. На рисунке 1.1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Множества изображены прямоугольниками, а результат операции выделен штриховкой.
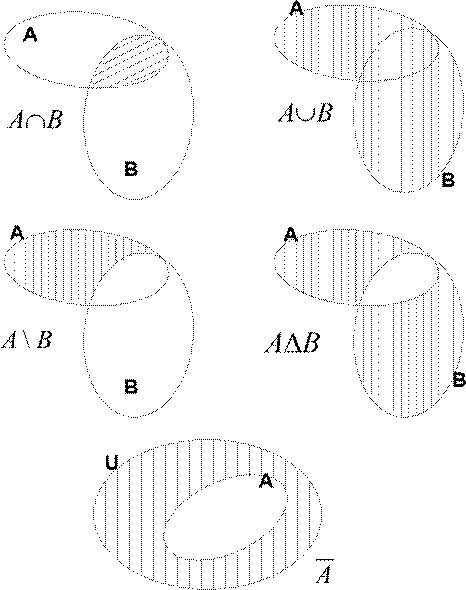
Рисунок 1.1
![]()
![]() Если мощность конечного
множества M , то мощность
множества всех его подмножеств 2
M .
Если мощность конечного
множества M , то мощность
множества всех его подмножеств 2
M .
Теорема позволяет подсчитать количество всех подмножеств конечного множества.
![]() У
множества M{1,2,3} восемь
подмножеств, то есть 2 M
=
23.
У
множества M{1,2,3} восемь
подмножеств, то есть 2 M
=
23.
A1 = {1,2,3}, A2 = { }1,2 , A3 = {1,3}, A4 = {2,3}, A5 = {1}, A6 = { }2 , A7 = { }3 , A8 = ∅.
Пусть универсум U – конечный, и число элементов в нем не превосходит разрядности ЭВМ:U<n. Элементы универсума нумеруются: U = {u1,u2,u3,K,un}.
Подмножество А универсума U представляется кодом (машинным словом или битовой шкалой), в котором каждый разряд:
⎧1,если ui ∈ A, ci = ⎨
⎩0,если ui ∉ A.
Код пересечения множеств А и В есть поразрядное логическое произведение кода множества А и кода множества В. Код объединения множеств А и В есть поразрядная логическая сумма кода множества А и кода множества В. Код дополнения множества А есть инверсия кода множества А. В большинстве ЭВМ для этих операций есть соответствующие машинные команды.
Для восьми подмножеств множества M{1,2,3}
A1 = {1,2,3}, A2 = { }1,2 , A3 = { }1,3 , A4 = {2,3}, A5 = {1}, A6 = {2}, A7 = {3}, A8 = ∅ можно составить трехразрядные двоичные коды : для А1 код – 111 для А2 код – 110 для А3 код – 101 для А4 код – 011 для А5 код – 100 для А6 код – 010 для А7 код – 001 для А8 код – 000
![]()
A1 ∩ A4 = {}1 = A5. Код для А1 – 1 1 1
Код для А4 – 0 1 1
___________________
Код пересечения - 0 1 1
____________________
Код дополнения - 1 0 0 ,что является кодом для А5 .
Пусть А и В – два множества. Декартовым произведением двух множеств
A×B называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит А, а второй принадлежит В:
A× B = {(a,b)| a∈ A∧ b∈ B}
Степенью множества А называют его декартово произведение самого на себя.
A2 = A× A.
Точка плоскости может быть задана упорядоченной парой координат, то есть двумя точками на координатных осях, изображающих множества рациональных чисел R. Таким образом, R2 = R× R.
![]() Теорема
A×
B =
A ×
B .
Теорема
A×
B =
A ×
B .
![]() Пусть A = {1,2,6} и B = {3,4}. A = 3, B =
2
Пусть A = {1,2,6} и B = {3,4}. A = 3, B =
2
![]() Декартово произведение
A×
B =
{(1,3),(1,4),(2,3),(2,4),(6,3),(6,4)}, A× B = 6 .
Декартово произведение
A×
B =
{(1,3),(1,4),(2,3),(2,4),(6,3),(6,4)}, A× B = 6 .
![]() Декартов квадрат B× B = {(3,3),(3,4),(4,3),(4,4)}, B× B = 4 .
Декартов квадрат B× B = {(3,3),(3,4),(4,3),(4,4)}, B× B = 4 .
Отношением R на множествах А и В называется подмножество их декартова произведения: R ⊂ A× B .
На множествах чисел хорошо известны отношения =,≤,<,>,≥,≠ . Например, отношение « больше » будет состоять из таких пар чисел
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.