Основные понятия алгебры логики. Элементарные функции алгебры логики. Свойства функций конъюнкции, дизъюнкции, отрицания

2   ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ

2.1 Элементарные функции алгебры логики

Основное понятие алгебры логики – высказывание. Высказывание – некоторое предложение, о котором можно утверждать, что оно истинно или ложно. Например, высказывание «Земля – это планета Солнечной системы» истинно, а о высказывании «на улице идет дождь» можно сказать , истинно оно или ложно, если указаны дополнительные сведения о погоде в данный момент.

Любое высказывание можно обозначить символом x и считать, что x=1, если высказывание истинно, а x=0 – если высказывание ложно.

Логическая (булева ) переменная – такая величина x, которая может принимать только два значения :  x={0,1}.

Высказывание абсолютно истинно, если соответствующая ему логическая величина принимает значение x=1 при любых  условиях. Высказывание абсолютно ложно, если соответствующая ему логическая величина принимает значение x=0 при любых  условиях.  Например, высказывание «Земля – спутник Марса» абсолютно ложно.

Логическая функция ( функция алгебры логики ) – функция  f( x₁, x_2, … , x_n), принимающая значение, равное нулю или единице на наборе логических переменных  x₁, x_2, … , x_n.

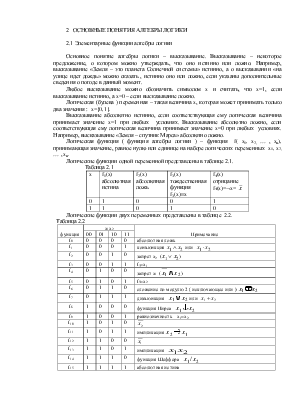
Логические функции одной переменной представлены в таблице 2.1.

Таблица 2.1

Логические функции двух переменных представлены в таблице  2.2.

Таблица 2.2

Две функции равносильны друг другу, если принимают на всех возможных наборах переменных одни и те же значения :

f₁( x₁, x_2, … , x_n)= f₂( x₁, x_2, … , x_n) .

Логические переменные могут быть действительными или фиктивными. Переменная x_i действительная, если значение функции f( x₁, … , x_i, … , x_n) изменяется при изменении x_i . Переменная фиктивна, если значение функции f( x₁, … , x_i, … , x_n) не изменяется при изменении x_i .

Например, функция f( x₁, x₂, x₃) =  , значения которой приведены в таблице 2.3.

Таблица 2.3

Из таблицы видно, что f( x₁, x₂, 0) = f( x₁, x₂, 1) для всех наборов x₁ и x₂ . Следовательно, x₃ – фиктивная переменная.

Использование фиктивных переменных дает возможность сокращать или расширять количество переменных для логических функций.

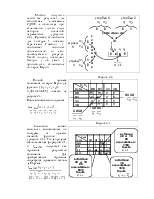
Впервые теория логических функций была применена П.С. Эренфестом к анализу контактных цепей (1910г.) . Возможность описания переключательных схем с помощью логических формул оказалась весьма ценной по двум причинам. Во-первых, с помощью формул удобнее проверять работу схем.  Во – вторых, задание условий работы любой переключательной схемы в виде формул упрощает процесс построения самой переключательной схемы, так как оказалось, что существует ряд эквивалентных преобразований, в результате которых логические формулы упрощаются. При описании переключательных схем замкнутое состояние контакта принимается за истинное высказывание, а разомкнутое – за ложное, поэтому последовательное соединение контактов можно рассматривать как функцию И ( конъюнкцию ), а параллельное -  как функцию ИЛИ ( дизъюнкцию ). Использование логических функций оказалось особенно полезным для описания работы логических элементов ЭВМ.

2.2 Свойства  функций конъюнкции, дизъюнкции, отрицания

Для конъюнкции, дизъюнкции и отрицания справедливы следующие восемь равенств. Пусть x – некоторая логическая переменная, тогда

1.  , что означает возможность замены в логическом выражении всех двойных отрицаний на исходные величины;

2.    и    , что позволяет сокращать длину логических выражений;

3.  ;

4.  ;

5.  ;

6.  ;

7.  ;

8.  .

Конъюнкция и  дизъюнкция обладают рядом свойств, аналогичных свойствам арифметических операций сложения и умножения.

9.  , и   -  ассоциативность;

10.  , и      -   коммутативность;

11.   , и   - дистрибутивность.

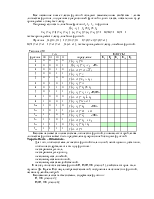
Можно доказать справедливость указанных свойств, сравнив таблицы истинности функций из левой и правой частей каждого равенства. Например, для последнего свойства, если обозначить F₁= и  F₂=, значения этих функций приведены в таблице 2.4

Таблица 2.4

Хорошо видно, что все значения F₁ и F₂ совпали на одних и тех же наборах значений переменных  x₁, x₂, x₃ .

Аналогично можно доказать и другие свойства.

12.   , и    - законы де Моргана;

13.   , и  = x₁  -  законы поглощения;

14.    -   свойство “склеивания”.

Законы де Моргана справедливы для любого количества переменных :

,

  .

В таблице 2.5 доказана справедливость свойства “склеивания” .

Таблица 2.5

2.3 Свойства функции сложения по модулю 2

Справедливы следующие свойства :

1.   ;

2.   ;

3.   ;

4.   ;

5.     -   коммутативность;

6.    - ассоциативность;

7.    - дистрибутивность.

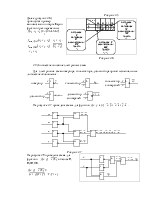
Конъюнкцию, дизъюнкцию, отрицание  можно выразить через сложение