Структура программных блоков и палитра «Программирование». Основные элементы программных блоков, страница 3

Программные блоки удобно использовать для определения в виде собственных функций отдельных этапов вычисления. Это удобно по причинам:

1)  Определение функции не влияет на вычисление в документе до тех пор пока функция не будет вызвана.

2)  Функция обладает свойствами универсальности т.к. подбором параметров её можно приспособить для решения многих задач, причём при вызове используются те имена параметров, которые нужны в данный момент.

3)  Функции – программные блоки, которые реализуют стандартные действия можно собрать в отдельный файл, который хранится отдельно от документа и в документе указывают только имя.

Подключение к документу других МС-документов. МС предоставляет возможность использовать в рабочем документе все элементы, записанные в другом документе, хранящемся на диске.

Для этого в текщий документ вставляется блок ссылки Reference to..

«Insert» - «Reference» («Вставка» - «Ссылка»).

После блока ссылки все действия в документе выполняются так, как если бы содержимое вставленного документа полностью набрано в текущем документе.

Примечание. Если содержимое библиотечного файла изменилось, то в открытом документе это не отображается. Для учета этих изменений нужно перезагрузить документ.

Механизм ссылок позволяет собрать в отдельном библиотечном файле все часто используемые константы, функции и другие элементы и использовать их для решения различных задач, подключая в случае необходимости. При этом рабочий файл разгружается, в нем остаются блоки, связанные с решением конкретной задачи. 

Это позволяет расширять возможности МС, создавая новые библиотечные файлы.

СОДЕРЖАНИЕ ЗАДАHИЯ

ЗАДАЧА 1. Составить функцию - программный блок,  выполняющую заданные действия (параметры задачи являются параметрами  функции). Если результат состоит  из нескольких величин, определить их как компоненты вектора результатов. Проверить работу функции на 2 тестовых примерах (ответ легко проверить), подобранных самостоятельно. Показать использование функции на 3 различных примерах, подобранных самостоятельно. 

1. В треугольнике известны сторона а и углы А, В и С (в градусах). Найти площадь треугольника, радиус вписанной окружности и полупериметр, используя формулы (для вычислений угол перевести в радианы):

S

                     ₂                                           r =

a sinBsinCS

          S =                                                              p =

                         2sin A                          ;     ,      где                        ^r .

2. В правильной треугольной пирамиде известны сторона основания а и угол α (в градусах) наклона боковой грани к плоскости основания. Найти объем и площадь полной поверхности пирамиды, используя формулы (для вычислений угол перевести в радианы):

V =1SоснH ;   Sполн =Sосн⎛⎜1+ 1 ⎞⎟,    где  Sосн =a² 3 ,  H = ^{a 3} tgα

                  3                                       ⎝      cosα⎠                          4                 6

3.  В треугольнике известны три стороны а, b, с. Найти (в градусах) углы этого треугольника, используя формулы:

b² + c² − a² bsin A cos A=    sin B =

                                  2bc        ;                    a      ;     C =180°− (A+B).

4.  В треугольнике известны стороны а, b, с. Найти радиус вписанной окружности и угол А (в радианах), используя формулы:

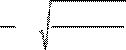
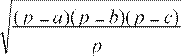         r =                                         _cos A ₌ p(p−a)           _{p =} a+b+c

                                                                ;           ^{2             bc}        ;  где             ²       .

5. В треугольнике известны три стороны а, Ь, с. Найти радиус описанной окружности и угол А (в радианах), используя формулы:

                                        abc                             A        (p −b)(p −c)                  a +b + c