Кинематический анализ. Структурная классификация плоских рычажных механизмов. Степень подвижности механизма

полные ускорения точки С во вращательном движении соответственно вокруг точек В и D определяются соотношениями:

,

.

На основании свойства подобия плана ускорений положение конца вектора абсолютного ускорения точки E шатуна найдем, если на отрезке  плана построим треугольник , подобный треугольнику  и сходственно с ним расположенный. Тогда:

.

Угловые ускорения ε₂ шатуна и ε₃ коромысла определим по касательным ускорениям  и :

;

.

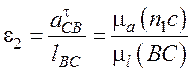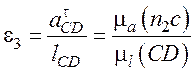Векторы ускорений  и , перенесенные с плана в точку С механизма, показывают направления угловых ускорений соответствующих звеньев на рис. 1.23, а направления  и  обозначены круговыми стрелками.

1.4.5. Кинематический анализ механизмов методом кинематических диаграмм

1.4.5.1. Построение диаграмм

Кинематические диаграммы представляют собой графическое изображение функциональной зависимости перемещения, скорости и ускорения точки или угла поворота, угловой скорости и углового ускорения вращающегося тела от заданного параметра. Если речь идет о движении точки или звена механизма, то этим параметром может быть либо время (кинематические диаграммы с параметром времени), либо обобщенная координата механизма – координата ведущей точки или угол поворота ведущего звена (кинематические диаграммы с параметром перемещений).

Диаграммы перемещений (линейных или угловых) могут быть получены в результате экспериментальных исследований или графических построений при решении задач по определению положений звеньев механизма за один цикл его движения.

Кинематические диаграммы скоростей и ускорений строят обычно либо по данным планов скоростей и ускорений, либо графическим дифференцированием диаграммы перемещений  или . Рассмотрим этот метод исследования применительно к конкретному механизму.

Построим диаграммы  и  для точки С ползуна центрального кривошипно-ползунного механизма (рис. 1.4.12, а), кривошип AB которого вращается с постоянной угловой скоростью .

Способом, изложенным в разделе 1.4.3, размечаем траектории точек В и С механизма. Отсчет перемещений точки С следует вести от одного из крайних положений ползуна, например, от левого.

По оси абсцисс системы координат ,  (рис. 1.4.12, б) отложим отрезок  (мм), изображающий в масштабе  [с/мм] время одного оборота кривошипа. Если угловая скорость кривошипа задана частотой  его вращения в минуту, то время одного оборота, выраженное в секундах:

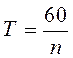
и, следовательно, масштаб времени:

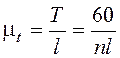.                                                                                                (1.4.8)

Отрезок  оси абсцисс делим на то же число равных частей, что и траекторию движения точки В.

Полученная кривая представляет собой диаграмму расстояний или удалений точки  от ее крайнего левого положения.

На ординатах, проведенных через точки 1, 2, 3, … , откладываем соответствующие расстояния, пройденные точкой С (рис. 1.4.12, а) от крайнего левого положения C₀ ползуна. Если отрезки C₀C₁, C₀C₂, ... брать непосредственно со схемы, то масштаб  диаграммы  по оси ординат будет равен масштабу  плана положений механизма.

Начиная с положения C₆, когда ползун займет крайнее правое положение, расстояния С₆С₇, C₆C₈,... вычитаем из ординаты (6-6')=C₀C₆.

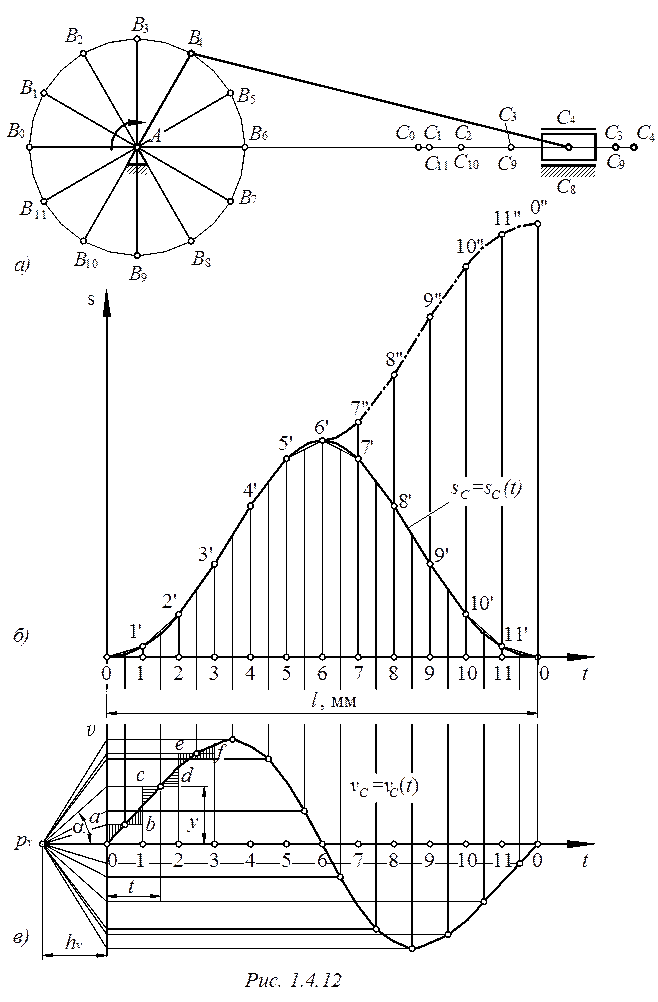
Чтобы построить диаграмму пути, пройденного точкой С за время одного оборота кривошипа без учета направления, то, начиная с положения 6, расстояния C₆C₇, C₆C₈, ... следует прибавлять к ранее отложенному отрезку C₀C₆ на рис. 1.4.12, б; эта часть кривой пути показана пунктиром.

Поскольку , то путь  точки В кривошипа, а также угол  его поворота пропорциональны времени . Следовательно, ось абсцисс на диаграмме будет также и осью линейного  и углового  перемещений. Таким образом, диаграмму  можно рассматривать и как диаграммы , . Масштабы  и  этих диаграмм по оси абсцисс соответственно равны:

,

.

1.4.5.2. Графическое дифференцирование (метод хорд)

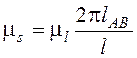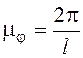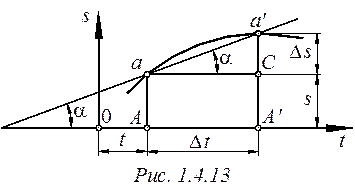На рис. 1.4.13 показан график функции , выражающей зависимость дуговой координаты движущейся точки от времени.

Координаты любой точки этой кривой, например точки а, могут быть выражены так:

;

.

Определим среднюю скорость движения за промежуток времени :

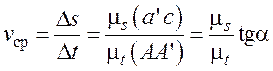                                                                  (1.4.9)

где       – угол, образуемый секущей (хордой)  с осью времени.

Аналогично по графику  может быть найдено среднее за рассматриваемый