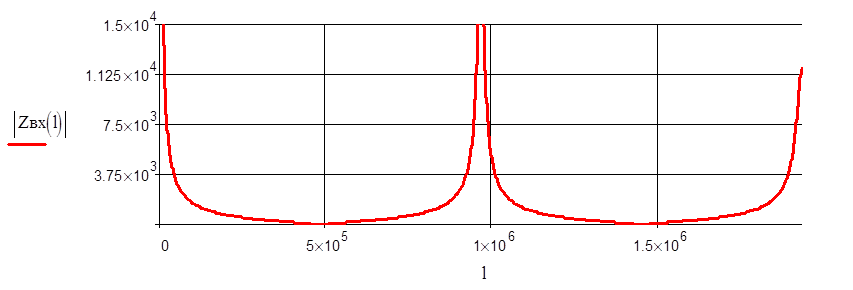
8. Считая, что линия Лехера является линией без потерь, построить для режима холостого хода кривые распределения мгновенных значений тока и напряжения вдоль линии на расстоянии, равном , для трёх моментов времени ( t1 = 0, t2 = /2, t3 = 3/2 ) при f = 100 Гц. Рассчитать и построить для этого режима зависимость входного сопротивления от длины линии.
![]()
![]() Для линии
без потерь:
Для линии
без потерь:
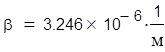 |
|||||||
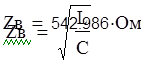 |
|||||||
![]() Напряжение на
входе:
Напряжение на
входе:
![]() В режиме холостого
хода входное сопротивление равно: (из п.4)
В режиме холостого
хода входное сопротивление равно: (из п.4)
![]() Напряжение выходе:
Напряжение выходе:
![]()
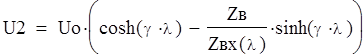
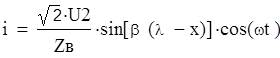 При холостом ходе
для линии без потерь уравнения напряжения и тока имеют вид:
При холостом ходе
для линии без потерь уравнения напряжения и тока имеют вид:
![]()
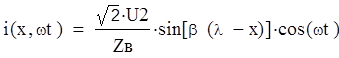
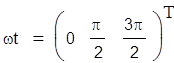
![]()
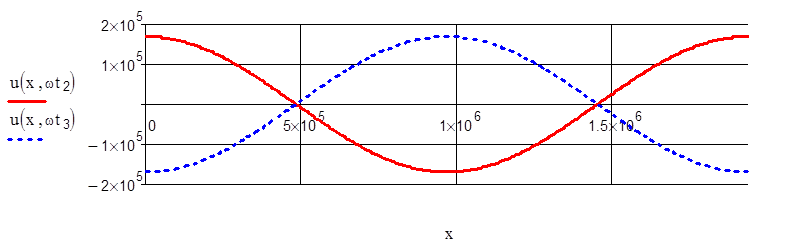
Графики токов и напряжений для заданных моментов времени:
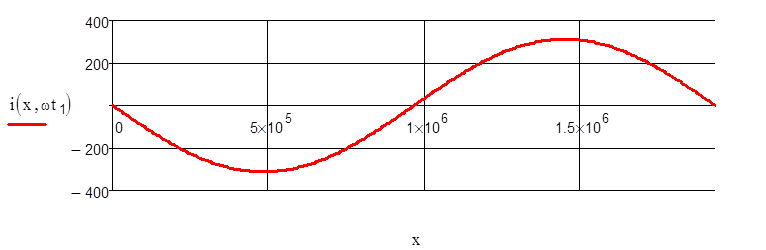
Задача 8.3 Рассчитать переходный режим линии задачи 8.2.
1. Найти волны, возникающие при подключении к заряженной до напряжения Uо линии Лехера нагрузки с сопротивлением rн. Построить эпюры напряжений и тока для момента времени, когда отраженная от конца линии волна пройдет расстояние, равное 0.25l.
![]()
![]()
![]()
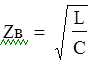 |
![]() Волновое
сопротивление:
Волновое
сопротивление:
В конце линии возникает обратная волна, движущаяся от конца линии к ее началу.
![]()
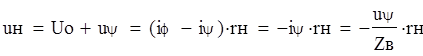
![]()
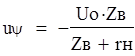
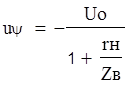
![]()
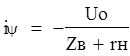
Суммарные напряжение и ток волны:
![]()
![]()
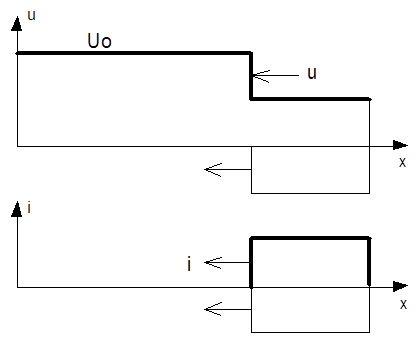
![]()
![]()
2. Рассчитать волны, возникающие при отключении источника от линии Лехера с сопротивлением нагрузки rн и установившимся током Iy = Uo/rн. Построить эпюры напряжений и токов для момента времени, когда отраженная волна пройдет расстояние 0.5*l.
![]()
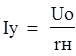
![]() Ток в начале линии
мгновенно спадет до нуля и возникнет волна с напряжением и током:
Ток в начале линии
мгновенно спадет до нуля и возникнет волна с напряжением и током:
![]()
![]()
![]()
![]()
![]()
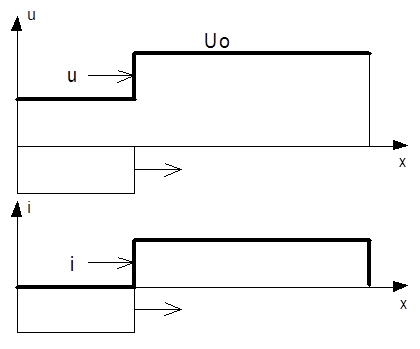
В результате наложения этой волны на предшествующий режим напряжение и ток в линии:
![]()
![]()
![]()
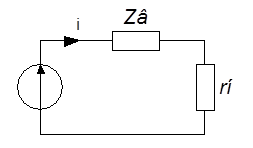
Вторая стадия. От конца линии к ее началу движется отраженная волна.
Схема замещения:
![]()
![]()
![]()
![]()
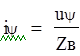
![]()
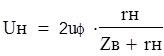
![]()
![]()
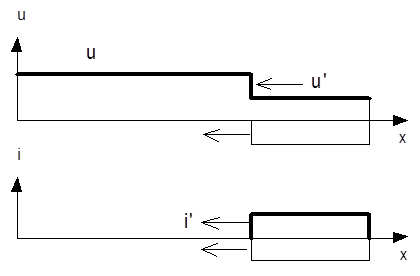
В результате наложения этой волны на предшествующий режим напряжение и ток в линии:
![]()
![]()
![]()
![]()
3. Определить волны, возникающие при подключении в точке х = 0.5*l нагруженной линии Лехера с сопротивлением нагрузки rн и установившимся током Iy = Uo/rн дополнительного приемника с сопротивлением rд = 0.5rн. Построить эпюры напряжений и токов для момента времени, когда волны от точки подключения пройдут расстояние 0.1*l.
![]()
![]()
![]()
![]()
При подключении нагрузки вправо и влево от места подключения пойдут равные по величине волны u = u, i = i. Ток в сопротивлении rд равен сумме токов обеих волн:
![]()
![]()
![]() Напряжение
на rд:
Напряжение
на rд:
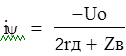 |
|||
![]()
![]() Находим
волны:
Находим
волны:
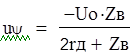 |
|||||
![]()
![]() Волна
справа от места включения:
Волна
справа от места включения:
![]()
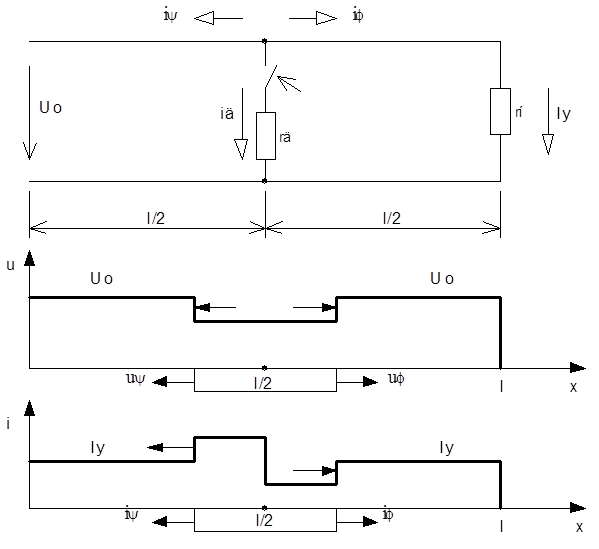
![]() Волна
слева от места включения:
Волна
слева от места включения:
 |
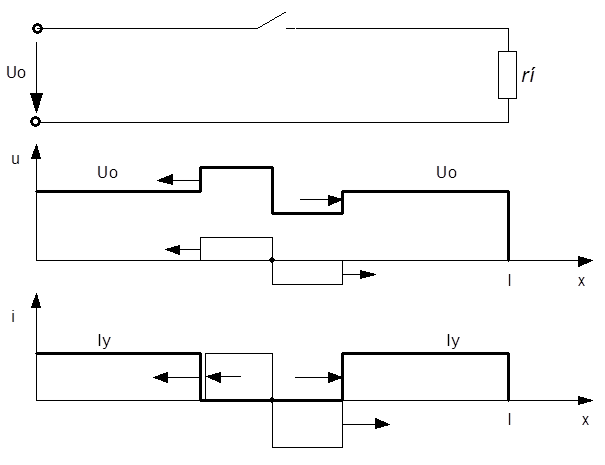
![]() 4. Найти волны,
возникающие при отключении нагруженной линии Лехера посередине. Построить эпюры
напряжений и токов для момента времени, когда волны пройдут от места
расположения выключателя расстояние 0.1*l.
4. Найти волны,
возникающие при отключении нагруженной линии Лехера посередине. Построить эпюры
напряжений и токов для момента времени, когда волны пройдут от места
расположения выключателя расстояние 0.1*l.
![]() После отключения
от места размыкания пойдет прямая волна с током, равным
После отключения
от места размыкания пойдет прямая волна с током, равным ![]() , и
напряжением
, и
напряжением ![]() , и
обратная волна с током
, и
обратная волна с током ![]() и
напряжением
и
напряжением ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() В результате
наложения этих волн на предшествующее распределение напряжения и тока на
участках слева и справа от места отключения ток уменьшается до нуля: ,
а напряжение на участке слева от еста отключения повышается до ,
а справа от этого места уменьшается до
В результате
наложения этих волн на предшествующее распределение напряжения и тока на
участках слева и справа от места отключения ток уменьшается до нуля: ,
а напряжение на участке слева от еста отключения повышается до ,
а справа от этого места уменьшается до
![]()
![]()
![]()
![]()
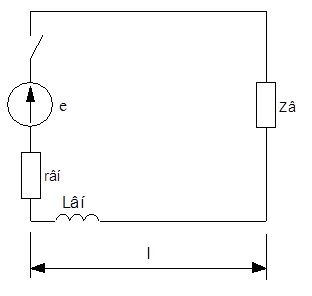 5. Определить
волны, возникающие в линии при подключении к ней источника постоянного
напряжения с ЭДС e = Uo, внутренним сопротивлением rвн и индуктивностью Lвн.
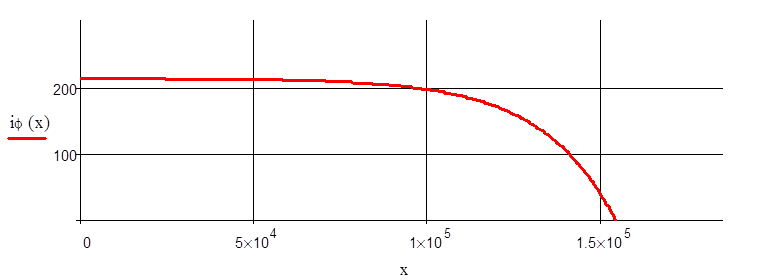
Построить эпюру распределения тока для момента времени, когда волна достигнет
точки с координатой x = 0.25*l.
5. Определить
волны, возникающие в линии при подключении к ней источника постоянного
напряжения с ЭДС e = Uo, внутренним сопротивлением rвн и индуктивностью Lвн.
Построить эпюру распределения тока для момента времени, когда волна достигнет
точки с координатой x = 0.25*l.
![]()
![]() Скорость волны:
Скорость волны:
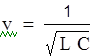
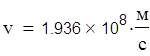
![]()
![]()
![]()
![]()
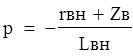
![]()
![]()
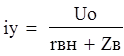
![]()
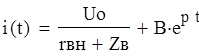
По закону коммутации: i(-0) = i(+0) = 0
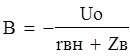
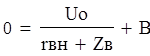
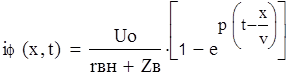
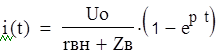
Ток падающей волны:
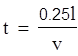 |
![]() Волна достигнет
точки с координатой x = в момент времени
Волна достигнет
точки с координатой x = в момент времени
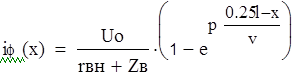 |
Тогда
![]() 6. Рассчитать
волны, возникающие в
линии Лехера при подключении к ней источника с синусоидальной ЭДС
6. Рассчитать
волны, возникающие в
линии Лехера при подключении к ней источника с синусоидальной ЭДС ![]() ,
внутренним сопротивлением rвн и индуктивностью Lвн. Частоту принять равной 50
Гц, начальную фазу -/6. Построить эпюру распределения волны тока для момента
времени, когда волна достигнет точки с координатой х = 0.5*l.
,
внутренним сопротивлением rвн и индуктивностью Lвн. Частоту принять равной 50
Гц, начальную фазу -/6. Построить эпюру распределения волны тока для момента
времени, когда волна достигнет точки с координатой х = 0.5*l.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.