решения данной задачи необходимо изучить теоретический материал параграфа 3.4 учебного пособия. Решение этой задачи не представляет большого труда, необходимо только сначала правильно графически изобразить три возможных взаимных расположения двух импульсов, после чего, найти соответствующие интегралы (рис.6). u( t ), v (t ) u( t),v(t) u(t) , v (t )
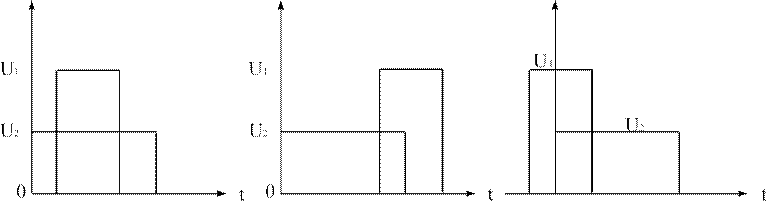
τ τ и 1 τ и 2 τ и1 τ τ и2 τ 0 τ и 1 τ и2
а ) б) в)
Рис.6 Варианты взаимного расположения импульсов.
Если вы все сделали правильно, то окончательная формула для расчета взаимокорреляционной функции будет выглядеть следующим образом:
U1U2τи1, 0 ≤τ≤τи2 −τи1 uv ( ) 2
B (τ) = U1U2 τи2 −τ, τи2 −τи1 <τ≤τи .
![]() U1U2(τи1 −τ),
−τи1 ≤τ< 0
U1U2(τи1 −τ),
−τи1 ≤τ< 0
Выполните аналитический вывод данной формулы, подставьте данные своего варианта и постройте график ВКФ.
1. Классификация радиотехнических сигналов. Описание сигналов посредством математических моделей.
2. Принцип динамического представления сигналов. Функция включения, динамическое представление сигнала посредством функции включения.
3. Дельта-функция, динамическое представление сигнала посредством δ-функции. Обобщенные функции.
4. Геометрические методы в теории сигналов. Линейное пространство сигналов, понятие координатного базиса. Нормированное линейное пространство, энергия сигнала. Метрическое пространство.
5. Скалярное произведение сигналов, ортогональные сигналы и обобщенные ряды Фурье. Примеры ортонормированных базисов.
6. Энергия сигнала, представленного в форме обобщенного ряда Фурье, оптимальность разложения сигнала по ортогональному базису.
7. Периодические сигналы и ряды Фурье, спектральная диаграмма периодического сигнала.
8. Комплексная форма ряда Фурье, изображение периодического сигнала на комплексной плоскости.
9. Периодическое продолжение импульса, преобразование Фурье, понятие спектральной плотности.
10. Физический смысл понятия спектральной плотности, обратное преобразование Фурье. Условие существования спектральной плотности сигнала.
11. Спектральные плотности прямоугольного и экспоненциального видеоимпульсов.
12. Спектральная плотность Гауссова видеоимпульса, дельта функции. Связь между длительностью импульса и шириной его спектра.
13. Основные свойства преобразования Фурье. Линейность, вещественная и мнимая части спектральной плотности. Спектральная плотность сигнала, смещенного во времени. Зависимость спектральной плотности сигнала от выбора масштаба измерения времени.
14. Спектральная плотность производной и неопределенного интеграла, спектральная плотность на выходе интегратора. Спектральная плотность произведения сигналов.
15. Обобщенная формула Рэлея, обобщение понятия спектральной плотности. Спектральная плотность постоянного во времени сигнала.
16. Спектральная плотность комплексного экспоненциального сигнала. Спектральная плотность гармонических колебаний. Спектральная плотность произвольного периодического сигнала.
17. Спектральная плотность функции включения, радиоимпульса.
18. Понятие комплексной частоты. Преобразование Лапласа, основные соотношения.
19. Взаимная спектральная плотность сигналов, энергетический спектр. Распределение энергии в спектре прямоугольного видеоимпульса.
20. Сравнение сигналов, сдвинутых во времени. Автокорреляционная функция сигнала.
21. АКФ неограниченно протяженного сигнала, связь между энергетическим спектром сигнала и его АКФ. Ограничения, накладываемые на вид АКФ сигнала.
22. Описание сложных сигналов с дискретной структурой, дискретная АКФ, примеры. Сигналы Баркера.
23. Взаимокорреляционная функция двух сигналов, принцип определения, свойства, примеры.
24. Связь ВКФ с взаимной спектральной плотностью. Обобщение понятия ВКФ на случай дискретных сигналов.
25. Системные операторы, классификация радиотехнических систем.
26. Импульсная характеристика системы. Интеграл Дюамеля, обобщение на многомерный случай. Условие физической реализации.
27. Переходная характеристика системы. Частотный коэффициент передачи.
28. АЧХ и ФЧХ. Ограничения, накладываемые на частотный коэффициент передачи, пример.
29. Системы, описываемые дифференциальными уравнениями, собственные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.