Дестабилизирующие факторы в спутниковых системах связи и вещания. Влияние рефракционных изменений атмосферы и ионосферы на траекторию волны, страница 3

где  - значение модуля коэффициента отражения в n-ом минимуме ; - значение угла места, соответствующее n-му минимуму. Из данного выражения следует, что интерференционные минимумы могут быть достаточно глубокими  при малых углах мета и низких частотах, на которых антенны земных станций имеют относительно широкие диаграммы направленности (), а значения  также могут быть близкими к единице из-за меньшего влияния неровностей поверхности Земли.

При малых D можно приближенно считать  для вертикальной и горизонтальной поляризации (см. **), исходя из чего согласно формулам (11.4.2) и (11.4.3) значения углов места в интерференционных минимумах будут равны

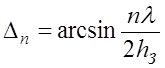                                 .                              (11.4.5)

Следует заметить, что число интерференционных минимумов всегда ограничено, так как максимальный угол места равен , что соответствует максимальной разности хода .

11.6.  Ослабление уровня сигнала за счет газов и гидрометеоров

Как уже рассматривалось в (5) на частотах выше 6-8 ГГц влияние поглощения в газах атмосферы, тумане и дожде на трассах Земля - ИСЗ становятся ощутимыми.

Величина поглощения в газах и тумане определяется согласно выражениям и графикам, приведенным в (5). 

Значение ослабления в дожде для трасс Земля – ИСЗ имеет некоторое отличие от наземных трасс.  В данном случае оно зависит не только от пространственной неравномерности дождя в горизонтальной плоскости, но и от вертикальной неоднородности.

Для трассы Земля – ИСЗ ослабление в дожде происходит на участке AD траектории волны, где точка D находится на пересечении с верхней границей дождя, расположенной  на  высоте   H_Д  (рис. 11.5).

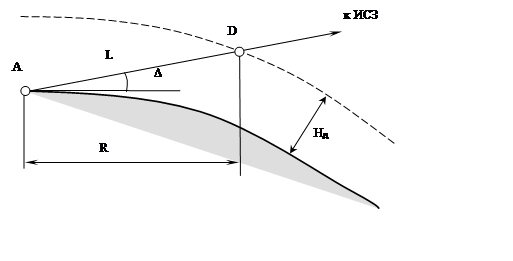Рис. 11.5. К пояснению ослабления в дожде на трассах Земля – ИСЗ

В [**] указывается, что в разных климатических зонах величина границы дождя расположена на высотах 7 – 15 км. Структура неоднородности пока еще полностью не изучена. Известно лишь, что с ростом высоты, в связи со снижением температуры  на 6 град/км, интенсивность дождя падает и при нулевой температуре переходит в твердое состояние, где поглощающие свойства резко падают. Из-за инерционности частицы становятся жидкими при более высокой температуре, примерно на высотах 2 – 3 км. В связи с отсутствием точных зависимостей интенсивности дождя по высоте принято использовать модель с равномерным распределение по высоте, с выстой границы H_Д» 3 км.

Исходя из принятых условий величина ослабления в дожде, в дБ, определяется из выражения

                           ,                        (11.5.1)

где   - значение погонного ослабления в дожде, дБ/км, при интенсивности дождя I_m;  - эквивалентная протяженность трассы, при которой ослабление в дожде с равномерной интенсивностью I_m оказывается  таким же, как и на реальной трассе Земля – ИСЗ при данном угле места D.

Учитывая однородность вертикальной интенсивности дождя можно  воспользоваться выражениями для наземных трасс, с учетом которых

                                     ,                                  (11.5.2)

где L- наклонная дальность траектории волны (см. рис. 11.5);

                                   ,                                 (11.5.3)

 - параметры модели пространственного распределения дождя в горизонтальной плоскости, а функция   определяется формулой

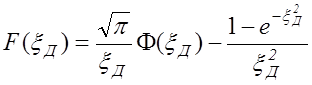                               ,                 (11.5.4)

 в которой  - интеграл  вероятности от аргумента .

Протяженность трассы в дожде определяется из выражения

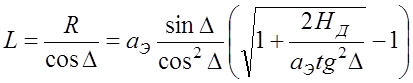                      ,         (11.5.5)

где а_Э » 8500 км – эквивалентный радиус Земли.

При малых D из формулы (11.5.5) получим

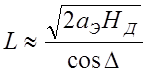                             ,                                     (11.5.6)

откуда

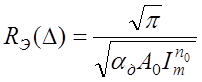                         .                               (11.5.7)

Следовательно при малых углах места D значение  не зависит от D  и H_Д.

При достаточно  больших углах места выражение (11.5.5) примет приближенный вид

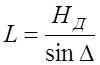                                      ,                                    (11.5.8)

и согласно (11.5.3)               

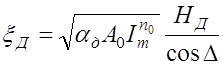                          .                           (11.5.9)

С учетом значений H_Д величина , при этом

и, следовательно,

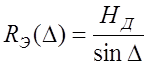                                          .                                  (11.5.11)

В данном случае эквивалентное расстояние  практически не зависит от интенсивности дождя.

В конечном итоге, по аналогии с наземной трассой (см. 5), вероятность появления значения множителя ослабления, определяемого выражением    (11.5.1), будет равно

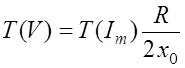                           .                               (11.5.11)

где  - вероятность появления дождя с интенсивностью I_m для определенного климатического района прохождения трассы; -  масштаб  пространственной  неравномерности    дождя;

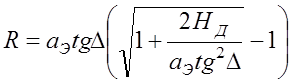                            .                        (11.5.12)

11.9.  Недостатки ССС, использующих ИСЗ на

         геостационарных  орбитах