Дестабилизирующие факторы в спутниковых системах связи и вещания. Влияние рефракционных изменений атмосферы и ионосферы на траекторию волны, страница 2

         поляризации волны в ионосфере

В результате действия магнитного поля Земли при прохождении волны через ионосферу происходи изменение ее плоскости поляризации.

Как известно, что линейно-поляризованную волну можно представить как суперпозицию двух волн с круговой поляризацией, с равными амплитудами, но противоположными направлениями вращения вектора напряженности электрического поля            (рис. 11.3).  Если свойства среды таковы, что скорость распространения и ослабления каждой из волн с круговой поляризацией одинакова, то их суперпозиция на любом расстоянии от источника дает вновь линейно-поляризованную волну с прежней пространственной ориентацией вектора .

 

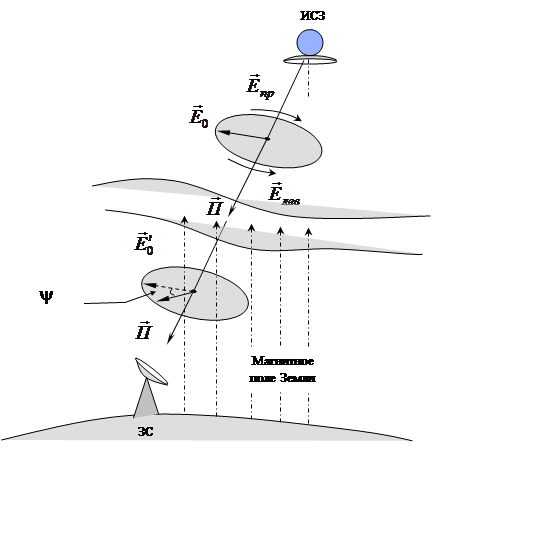Рис. 11.3.  К пояснению эффекта Фарадея

В случае действия постоянного магнитного поля Земли на движущиеся электроны в ионосфере будет действовать сила Лоренца, заставляя двигаться их по спиральным траекториям. Такое явление (по аналогии с оптическим) называют эффектом Фарадея. Поэтому для линейно-поляризованной волны, каждая из ее составляющих будет находиться в разных условиях: для одной направление вектора вращения будет совпадать с направлением движения электронов, для другой оно будет обратным. В связи с чем скорости распространения и поглощения волны в ионосфере будут различными, и по мере прохождения волны в ионосфере их амплитуды и фазы будут меняться различным образом.  Суперпозиция  этих волн уже не дает исходной линейно-поляризованной волны, волна будет эллиптически поляризованной, а пространственная ориентация эллипса будет также меняться по мер распространения волны.

При достаточно высоких частотах, которые применяются в ССС, поглощением волны в ионосфере можно пренебречь, в связи с чем за счет эффекта Фарадея будут меняться в основном только фазы составляющих с круговой поляризацией. Их суперпозиция даст линейно-поляризованную волну, но из-за разности фаз составляющих пространственная ориентация вектора  будет иной по сравнению с первоначальной (см. рис. 11.3), что при использовании линейно-поляризованных антенн приводит к потере уровня сигнала, величину которых можно определить по формуле [**]

,                                               (11.3.1)

где y - угол поворота поляризации (сдвиг фазы сигнала)

.                                           (11.3.2)

Результаты расчетов показывают, что эффект Фарадея приводит к изменению вектора поляризации на частотах f£5ГГц.  При  f =2 ГГц y=6…18⁰, при f=5 ГГц  y=1…3⁰, а при f³ 10 ГГц оно пренебрежимо мало: y=0,1…0,3⁰.  Для устранения влияния этого эффекта на частотах f < 10 ГГц в ССС применяют антенны с круговой поляризацией. Хотя их усиление по мощности на 3 дБ меньше, чем у антенн с линейной поляризацией. Предпочтение антеннам с круговой поляризацией связано с тем, что в них отсутствуют потери из-за несогласованности поляризации приемной и передающей антенн.

11.4.  Запаздывание сигналов в ССС

При .

Для дуплексной связи – теряется эффект присутствия.

При использовании стыков 4пр-2пр. из-за отражений неразборчивость речи.

Для защиты используют «эхо-заградители».

11.5.  Влияние отражений от земной поверхности

В спутниковых системах связи в направлении ИСЗ – Земля в точку приема приходят основная и отраженная от земной поверхности волны (рис. 11.4), в результате интерференции которых может произойти как замирание, так и увеличение уровня сигнала. 

 

Рис. 11.4.  К пояснению влияния отраженной от Земли волны

Выражение, определяющее множитель ослабления сигнала в результате влияния Земли (аналогично наземным радиолиниям) можно записать в следующем виде:

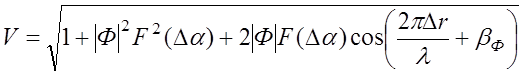          , (11.4.1)

где ,  - модуль и фаза коэффициента отражения от земной поверхности при данном значении угла скольжения ;  - ослабление амплитуды отраженной волны за счет диаграммы направленности антенны земной станции; - разность хода между прямой и отраженной волнами.

Так как антенны земной станции, как правило, располагают невысоко от Земли, точка отражения будет располагаться на небольшом расстоянии R₁ от станции. Поэтому кривизной Земли можно пренебречь, считая ее приближенно плоской. При таком приближении можно считать, что , . Откуда

                                           .                                 (11.4.2)

где  - высота антенны земной станции (см. рис. 11.4); - угол места оси главного лепестка антенны земной станции.  Согласно выражению (11.4.1) интерференционные минимумы будут наблюдаться при

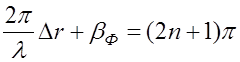                                      ,                      (11.4.3)

где n = 1, 2, 3, … - номер минимума. Величина множителя ослабления в этих минимумах согласно формуле (11.4.1) будет равна

                                         ,                          (11.4.4)