Расчет цифрового фильтра методом билинейного z-преобразования. Получение схемы данного фильтра. Реализация в программе MatLab 6.1

Министерство образования Российской Федерации

Дальневосточный Государственный Технический Университет

(ДВПИ им. Куйбышева)

Курсовая работа

по дисциплине «Теория электрической связи»

на тему:

«Расчет цифрового фильтра методом билинейного z-преобразования. Получение схемы данного фильтра. Реализация в программе MatLab 6.1»

                                       Выполнил: студент группы Р-4011

   Проверил: 

Владивосток 2006 г.

Задание:

Целью данной курсовой работы является разработка цифрового фильтра из аналового фильтра. Далее необходимо реализовать схему полученного фильтра в программе MatLab 6.1. Для расчета используют 3 вида фильтров: фильтр Баттерворта, фильтры Чебышева I и II рода. Так же необходимо выбрать неравномерность фильтра (в дБ) из ряда значений: 0,1; 0,5; 1; 2; 3. Для удобства расчета частота дискретизации выбирается как 2 частоты среза, в свою очередь частота среза определяется как произведение 10³ на последнюю цифру зачетной книжки. Выбор фильтра производится сложным математическим способом. Для моего варианта используется фильтр Чебышева I рода с неравномерностью в 2 дБ.

Решение:

Метод билинейного z-преобразования позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового типа. Частотный коэффициент передачи для данного варианта:

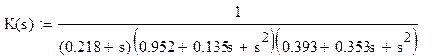
Функция передачи аналоговой цепи с сосредоточенными параметрами представляет собой дробно-рациональную функцию переменной S. Чтобы получить функцию передачи дискретного фильтра, необходимо перейти из s-области в z-область, при чем дробно-рациональный характер должен сохранится. Поэтому замена для переменной s должна представлять собой также дробно-рациональную функцию переменной z. Чтобы частотные характеристики аналогового и дискретного фильтров были связаны простой зависимостью, искомая замена переменной должна отображать мнимую ось в s-области на единичную окружность в z-области. Переход в виде формулы осуществляется по следующей формуле:

,где f_d- частота дискретизации,

f_sr- частота среза. f_sr= 6000 Гц

Для нахождения частотной характеристики дискретного фильтра используют связь между частотными характеристиками:

Общий вид частотной характеристики дискретного фильтра выглядит следующим образом:

H(z) = (a₀ + a₁z^-1 +…+ a_mz^-m) / (1 – b₁z^-1 -…- b_nz^-n)

Числитель данного выражения является нерекурсивной частью и описывает конечную импульсную характеристику (КИХ). А само отношение является рекурсивной частью и описывает бесконечную импульсную характеристику (БИХ).

Теперь для получения частотной характеристики необходимо подставить одно выражение в другое выражение. Далее проводя сложные математические преобразования в программе MathCad 11, получаем следующие выражения для коэффициентов:

Итак конечное выражение для частотной характеристики дискретного фильтра выглядит следующим образом:

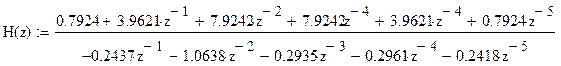
Теперь мы можем выписать из последнего выражения коэффициенты для всех усилителей схемы дискретного фильтра. С помощью программы MatLab соберем схему фильтра, которая нам необходима:

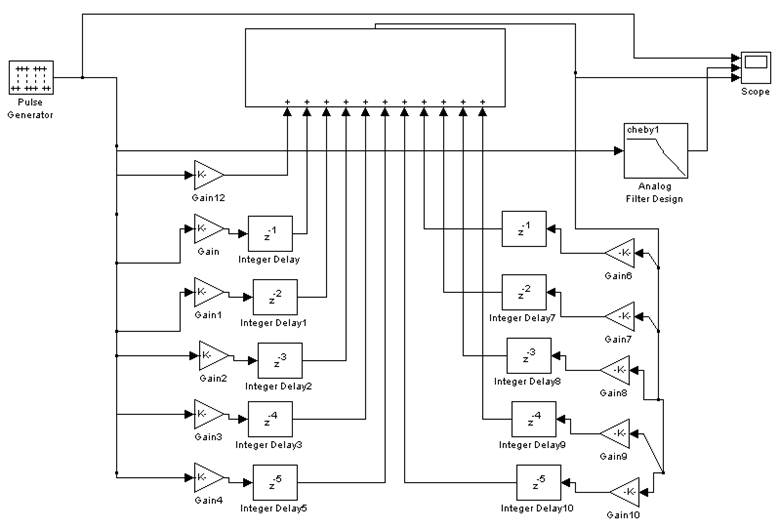
Далее я рассмотрю элементы, входящие в схему данного фильтра:

Данный блок называется Pulse Generator. Он служит для выработки нужного нам импульса. Свойства этого блока представлены ниже:

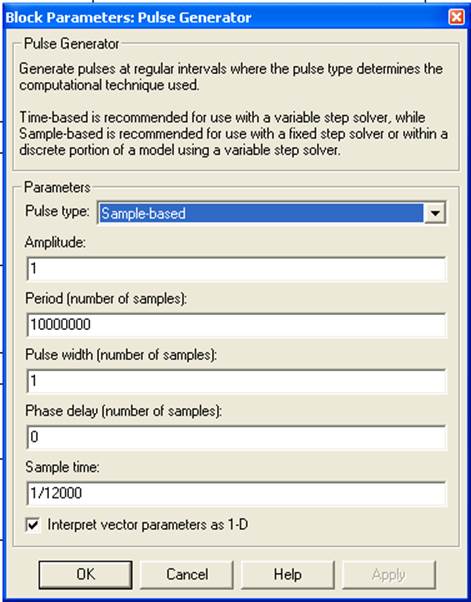Amplitude – амплитуда сигнала.

Period – количество сэмплов.

Pulse width – ширина импульса.

Sample time - период

Следующий блок это Gain,то есть усилитель:

 Этот блок имеет лишь один параметр – коэффициент усиления / ослабления.

Этот блок называется сумматор. Его предназначение заключается в сложении / вычитании сигналов.

 Этот блок используется в качестве линии задержки. Характеризуется лишь показателем степени. Это число и показывает на сколько тактов задерживается сигнал.

Теперь рассмотрим принцип работы такой схемы:

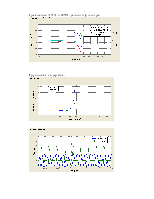
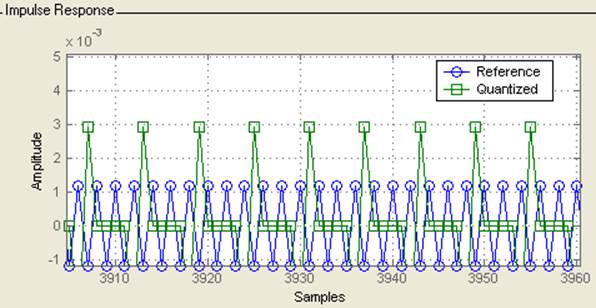
Импульс, идущий от блока Pulse Generator разделяется на части. Каждая часть, пройдя через свой усилитель, попадет на блок линии задержки (Integer Delay). После этого, каждая часть попадает на сумматор. Данная часть схемы называется нерекурсивной частью цифрового фильтра. На сумматоре происходит складывания этих частей импульса. Далее, импульс идёт на осциллограф, при этом импульс снова разделяется на части, каждая из которых, пройдя через свой усилитель попадает на очередную линию задержки. Вторая серия усилителей и линий задержки называется рекурсивной частью фильтра. После линий задержки импульсы снова попадают на сумматор. Ну а далее всё происходит по вышеописанной схеме. Ниже приведены показания осциллографа. На верхнем входе мы наблюдаем импульс, идущий напрямую от блока Pulse Generator. На втором входе представлен сигнал пропущенный через фильтр Чебышева 1 рода, взятого из пакета MathLab 6.1. На третьем входе, мы видим сигнал пропущенный через наш цифровой фильтр.

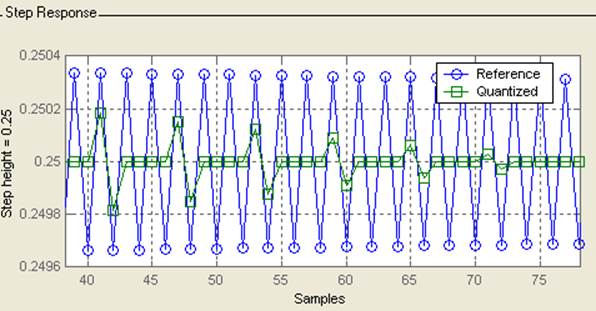
Далее приведены показания характеристик нашего фильтра:

Непосредственно сам фильтр:

АЧХ:

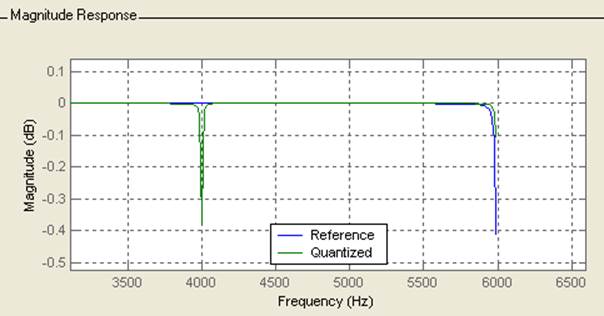
ФЧХ:

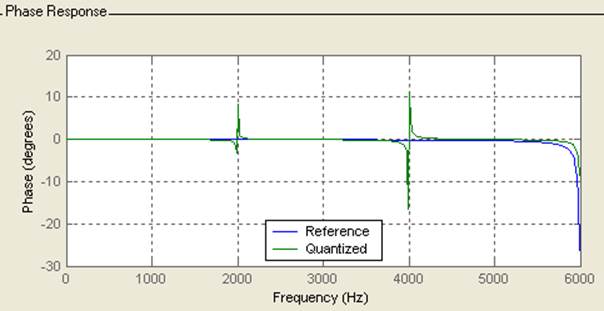
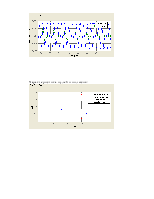
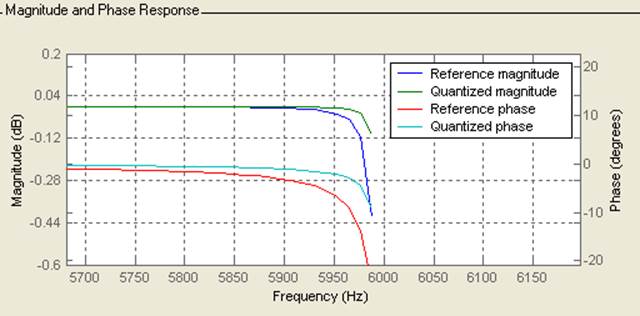
Сравнение АЧХ и ФЧХ данного фильтра:

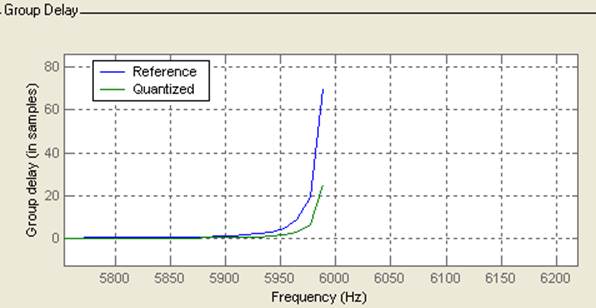
Групповая задержка:

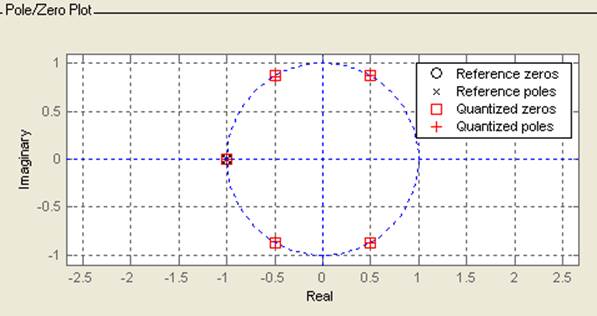
Характеристика нулей и полюсов:

Список литературы:

1.  Сергиенко А.Б. Цифровая обработка сигналов: Учебник для вузов.

2.  Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы: Учебник для вузов. – М.: Радио и связь, 1994.

3.  Баскаков С.И. Радиотехнические  цепи и сигналы: Учебник для вузов. – М.: Высш. шк., 2000.