Обобщенная структурная схема систем электросвязи, подсистемы и классификация. Линейное и нелинейное преобразование сигналов

Пусть  передаточная функция аналогового фильтра, задаваемая дробно-рациональным выражениям по степеням комплексной частоты p. К системной функции H(z)  проектируемого цифрового фильтра можно перейти сделав в  замену вида:

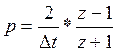
В этом фактически и заключается процедура синтеза ЦФ методом инвариантных частотных характеристик. Полученная при этом системная функция ЦФ оказывается дробно-рациональной и поэтому позволяет записать алгоритм цифровой фильтрации  ( см. раздел “Реализация алгоритмов цифровой фильтрации” ).

Синтез линейного цифрового фильтра.

Синтез линейного ЦФ рассмотрим на примере фильтров нижних частот (ФНЧ). К фильтрам других типов (верхних частот, полосовым, заграждающим ) можно будет легко перейти путем не сложных преобразований выражений для ФНЧ.

Идеальная частотная характеристика ФНЧ с частотой среза  ( см. рис. 2) заведомо нереализуема, ее необходимо аппроксимировать.

0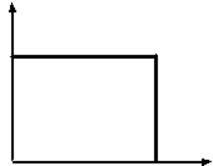

Рис. 2. Идеальная частотная характеристика ФНЧ с частотой среза

Мы рассмотрим два вида аппроксимации – максимально-плоскую и чебышевскую.

Максимально-плоская аппроксимация

Данный способ построен на использовании коэффициента передачи мощности вида.

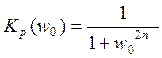
где - безразмерная нормированная частота, целое число n=1, 2, 3,...-порядок фильтра. Фильтры такого типа называют фильтрами с максимально-плоской характеристикой или фильтрами Баттервота.

Перейдем теперь к передаточной функции K(p) введя в рассмотрение нормированную комплексную частоту  и перепишем (4) так:

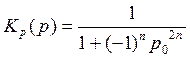
На плоскости  функция  имеет 2n  полюсов, которые являются корнями уравнения

Все эти корни лежат на окружности единичного радиуса с центром в начале координат. Правило нахождения корней такого. Все полюсы расположены на одинаковом угловом расстоянии друг от друга, равном ;

Если n- нечетно, то первый корень  если n- четно, то .

Те полюсы, которые расположены в левой полуплоскости, отвечают синтезируемому  фильтру. Их зеркальное отображение в правой полуплоскости  не принимается во внимание. Таким образом, получаем n комплексных корней и  можно представить в виде:

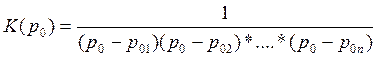
Чебышевская аппроксимация.

Здесь коэффициент передачи мощности задается выражением:

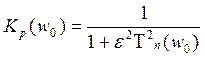
где -константа, коэффициент неравномерности характеристики в полосе пропускания, - многочлен Чебышева n-го порядка:

Функция  при любом n может быть найдена из рекуррентного соотношения:

причем  и

В предела полосы пропускания значение  колеблется в пределах от 1до , если , то ФНЧ обеспечивает большое ослабление сигнала.

Как видно из (5), полюсы коэффициента передачи мощности чебышевского фильтра являются конями уравнения           

Для вычисления его корней сначала вычисляется вспомогательный параметр:

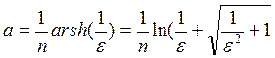
Затем должны быть найдены полюсы фильтра Баттерворда того же порядка.

Переход к полюсам чебышевского фильтра осуществляется умножением абсциссы каждого полюса фильтра Баттерворда на sha, а ординаты- на cha.

Получив координаты полюсов, можно записать выражение передаточной функции ФНЧ Чебышева в виде

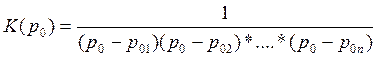
Таким образом, в случае обеих аппроксимаций проходим к дробно-рациональной записи передаточной функции ФНЧ, разница лишь в значении корней Дальнейшие выкладки являются общими для обоих типов ФНЧ.

Теперь нужно перейти к истиной комплексной частоте p, сделав замену переменных в выражении для  вида  где - частота среза аналогового фильтра-прототипа. Тогда

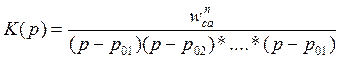
Затем находим системную функцию H(z) сделав замену переменных в последнем выражение:

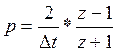
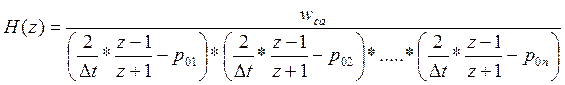
Приведя системную функцию H(z) к «каноническому» виду

(рекурсивный фильтр), получаем коэффициенты ЦФ. Данный факт говорит о том, что ЦФ построен, т.к уже можно непосредственно записать алгоритм линейной цифровой