Расчёт цифрового фильтра нижних частот. Построения схемы цифрового фильтра нижних частот в программном пакете MATLAB 6.5

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ

ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

(ДВПИ имени В. В. Куйбышева)

ИНСТИТУТ РАДИОЭЛЕКТРОНИКИ, ИНФОРМАТИКИ И ЭЛЕКТРОТЕХНИКИ

Кафедра РТС

Пояснительная записка к курсовой работе на тему

«Расчёт цифрового фильтра нижних частот»

по курсу «Теория электрической связи».

Выполнил: студент группы Р-5011

Проверил:

преподаватель

Владивосток 2007

Содержание.

Задание на курсовую работу………………………………………………………..2

Исходные данные……………………………………………………………………3

Расчётная часть……………………………………………………………………....4

Построения схемы цифрового фильтра нижних частот в программном пакете MATLAB 6.5…………………………………………………………………………7

АЧХ и ФЧХ фильтра……………………………………………………………….13

Импульсная характеристика фильтра……………………………………………..13

Задание на курсовую работу.

Вариант №21.

Рассчитать цифровой фильтр нижних частот 6-ого порядка (n=6) методом билинейного z-преобразования.

Варианты:

·  Фильтр Баттерворта;

·  Фильтр Бесселя;

·  Фильтр Чебышева 1-ого рода (мой вариант фильтра).

Выбор частоты дискретизации фильтра : № варианта умножается на 1000;

Выбор частоты среза фильтра : .

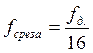Для фильтра Чебышева 1-ого и 2-ого  рода существует параметр «неравномерность частотной характеристики». Его значение выбрать равным 1дБ.

Задание:

1.  Получить системную функцию цифрового фильтра H(z);

2.  Получить схему фильтра в MATLAB 6.5;

3.  Построить АЧХ исходного аналогового фильтра;

4.  Построить импульсную характеристику h(t) для исходного аналогового и цифрового фильтров;

5.  Построить ФЧХ цифрового фильтра;

6.  Сравнить импульсные характеристики аналогового и цифрового фильтров;

7.  Рассчитать принципиальную схему фильтра 6-ого порядка на основе ОУ (схему построить в программе Electronics Workbench).

Все пункты за исключением последнего необходимо реализовать в программе MATLAB 6.5. Также нужно сравнить полученный цифровой фильтр с аналогичным фильтром, предложенным в программе.

Исходные данные.

Частотный коэффициент передачи (n=6):

;

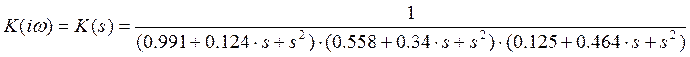Частота дискретизации фильтра:

;

Частота среза фильтра:

;

;

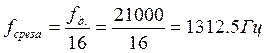Добротности полюсов:

; ; .

Расчётная часть.

Метод билинейного z-преобразования позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового прототипа.

Функция передачи аналоговой цепи с сосредоточенными параметрами представляет собой дробно-рациональную функцию переменной s. Чтобы получить функцию передачи дискретного фильтра, необходимо перейти из s-области в z-область, причем дробно-рациональный характер функции должен сохраниться. Поэтому замена для переменной s должна представлять собой также дробно-рациональную функцию переменной z. Чтобы частотные характеристики аналогового и дискретного фильтров были связаны простой зависимостью, искомая замена переменной должна отображать мнимую ось в s-области на единичную окружность в z-области. В этом случае частотные характеристики аналогового и дискретного фильтров будут связаны лишь трансформацией частотной оси и никаких искажений «по вертикали» не будет.

Простейшей из функций, удовлетворяющих перечисленным требованиям, является  билинейное z-преобразование (bilinear transformation).

Мне дана передаточная функция для фильтра Чебышева 1-ого рода 6 порядка (n=6):

;

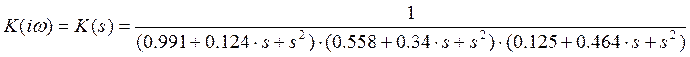Для нахождения частотной характеристики дискретного фильтра используют связь между частотными характеристиками:

;

Общий вид частотной характеристики дискретного фильтра выглядит следующим образом:

;

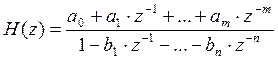Числитель данного выражения является нерекурсивной частью и описывает конечную импульсную характеристику (КИХ). А само отношение является рекурсивной частью и описывает бесконечную импульсную характеристику (БИХ).

Запишем наш коэффициент передачи, используя :

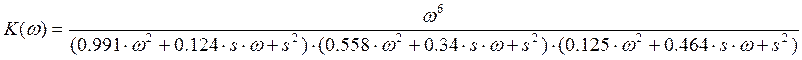
Далее в выражении необходимо произвести следующую замену:

;

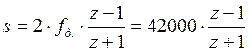Для окончательного перехода к системной функции цифрового фильтра H(z) необходимо привести выражение к виду:

;

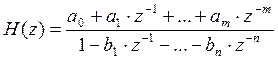Далее все математические операции и преобразования выполняются в математическом пакете Maple 9:

> w:=2*3.14*1312.5;

> H:=w^6/((0.991*w^2+0.124*w*s+s^2)*(0.558*w^2+0.34*w*s+s^2)*(0.125*w^2+0.464*w*s+s^2));

> s:=2*21000*(z-1)/(z+1);

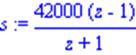
> F:=simplify(H);

> A:=expand(0.1045279613e31*(z+1.)^6);

> B:=expand((0.6247514323e11*z^2-0.1131115095e12*z+0.5961334723e11)*(0.1919612754e12*z^2-0.3452180292e12*z+0.1684206954e12)*(0.1933122191e13*z^2-0.3511015298e13*z+0.1611862511e13));