Переизлучение электромагнитной энергии от неоднородностей атмосферы. Отражение от неоднородностей атмосферы. Коэффициенты отражения

Лекция 4: ПЕРЕИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОЙ        

                ЭНЕРГИИ ОТ НЕОДНОРОДНОСТЕЙ АТМОСФЕРЫ

План занятия:

4.1 Отражение от неоднородностей атмосферы. Коэффициенты отражения

При распространении радиоволн в неоднородной земной атмосфере, помимо процесса преломления радиоволн, происходит процесс переизлучения электромагнитной энергии, т.е. энергия распространяется не только в направлении основной волны.

Процесс переизлучения электромагнитной энергии в сферической-слоистой неоднородной атмосфере сводится к генерации отраженной волны при распространении проходящей волны через толщу атмосферы.

Так как радиус сферичности земной атмосферы очень велик, а расстояние от границы раздела до источника и точки приема всегда значительно больше длины волны, возможно применение приближенной модели с плоской волной (рис. 4.1).

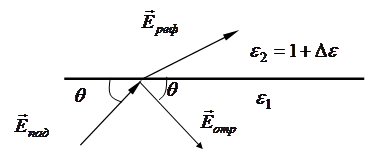Рис. 4.1. К пояснению процесса отражения радиоволн в атмосфере

В этом случае применимы френелевские формулы коэффициентов отражения плоской волны от границы раздела двух неоднородных сред. Если первая среда имеет  диэлектрическую проницаемость , а вторая – значение  и из первой среды падает плоская волна (см. рис. 4.1), вектор напряженности электрического поля которой  параллелен  плоскости раздела (горизонтальная поляризация), то коэффициент отражения  , будет равен

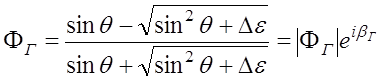,                         (4.1.1)

где - угол скольжения, т.е. угол между плоскостью раздела и направлением падающей волной (см. рис. 4.1). При вертикальной поляризации, когда вектор  лежит в плоскости, перпендикулярной плоскости раздела, коэффициент отражения определяется выражением

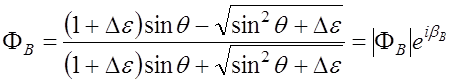                .          (4.1.2)

В земной атмосфере перепады диэлектрической проницаемости очень малы , поэтому формулы (4.1.1) и (4.1.2) приводятся к одинаковому приближенному выражению:

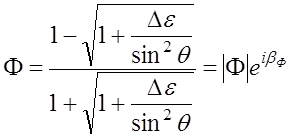              ,                           (4.1.3)

т.е. при  коэффициент отражения не зависит от вида поляризации волны.

В случае, если величина  отрицательна и удовлетворяет неравенству

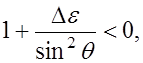                                                                 (4.1.4)

то , т.е. имеет место полное отражение, а фаза коэффициента отражения при этом равна

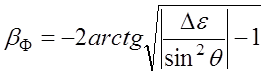                           .                               (4.1.5)

В случае, когда  любого знака, но при выполнении неравенства

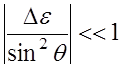                                                                         (4.1.6)

коэффициент отражения согласно формуле (4.1.3) приближенно равен

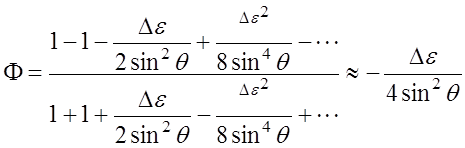        .                (4.1.7)

Если в данном случае , то , а при  .

4.2 Отражение радиоволн от слоев и полупространства

Представим околоземнуют атмосферу в виде бесконечно протяженного в горизонтальном направлении слоя толщиной , с некоторым распределением диэлектрической проницаемости , на нижнюю границу которого под углом скольжения  падает плоская волна (рис. 4.2). Разобьем слой на тонкие слои толщиной , настолько тонкие, что в пределах каждого слоя можно считать величиной постоянной. На границах раздела между такими тонкими слоями   претерпевает скачек

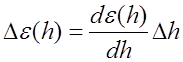                      .                                        (5.2.1)

То есть, предположим скачкообразное изменение  на границах между такими слоями: плавная зависимость  заменена ступенчатой (см. рис. 4.2).

			h

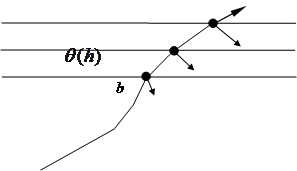
Рис. 4.2.   К пояснению процесса отражения от слоя  неоднородной атмосферы

При прохождении волны в слое происходит ее преломление. При скачкообразном изменении  траектория волны представляются ломанной линией, наклон которой по отношению к нижней границе слоя будет уменьшаться в тех областях слоя, где  уменьшается и возрастать, где  увеличивается.  В пределе, когда  линейно - ломанная траектория превратиться в плавную кривую.

Кроме того, от каждой границы между тонкими слоями будет происходить отражение и напряженность поля отраженной волны  можно представить в виде геометрической суммы

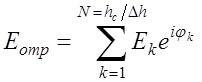                      ,                                     (4.2.1)

где и - соответственно, амплитуда и фаза волны, отраженной от k-й границы.

В нашем случае функция  меняется достаточно медленно, это позволяет значительно упростить вывод формулы для коэффициента отражения. Так как  в этом случае, согласно формуле (4.2.1) будет удовлетворять условиям (4.1.6), амплитуду волны отраженной от k-й границы, можно определить, воспользовавшись приближенной формулой (4.1.7):

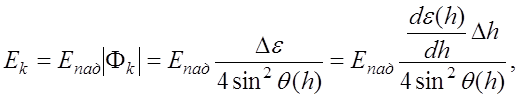                (4.2.3)

где через h обозначена высота k-й границы (см. рис.2).

Учитывая достаточно малое изменение угла скольжения,   примем приближение при выводе формулы: пологая, что угол скольжения для любой границы постоянен (). Данное приближение корректно, так как в дальнейших расчетах используется эквивалентный радиус Земли, учитывающий явление рефракции.

При выполнении условий (4.1.6) коэффициент отражения от любой k-й границы будет очень малым, поэтому можно пренебречь в пределах слоя h_c изменением амплитуды падающей волны на k-ю границу, за счет отражения от предыдущих (k-1) границ.

Принимая фазу отраженной от нижней границы волны за нулевую, определим относительную фазу волны, отраженной от k-й границы

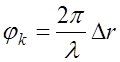                                  ,                                       (4.2.4)

где - разность хода между длиной пути волны, отраженной от k-й границы