Влияние рельефа местности на распространение УКВ. Причины ослабления напряженности поля поверхностных волн для случая гладкой сферической Земли

4 часа

Лекция 6:    ВЛИЯНИЕ РЕЛьЕФА МЕСТНОСТИ НА              

                  РАСПРОСТРАНЕНИЕ УКВ

План занятия:

6.1. Причины ослабления напряженности поля поверхностных волн для случая гладкой сферической  Земли

В реальных условиях Земля представляет собой сложную структуру поверхности, имеющую неровности: холмы, горы волнение моря, различную растительность и местные предметы (строения и пр.). Учет всех этих факторов значительно осложняет методы проектирования радиотрасс. Поэтому большое практическое применение имеют приближенные методы, учитывающие лишь основные особенности местности, которые могут давать достаточно точные для практики результаты при определенных типичных условиях.

Ранее (в Лекции 3) было показано, что при распространении радиоволн в пределах прямой видимости на напряженность поля в точке приема оказывают влияние только те среды, которые попадают в существенную область пространства. В диапазоне УКВ существенная область представляет собой вытянутый эллипс, в которой большая ось более чем сотни раз превышает малую ось, в результате чего (чаще всего) влияние радиуса кривизны препятствий, попадающих в существенную область пространства, будет несущественно, если этот радиус значительно больше малой оси эллипсоида.  С учетом этого, все основные методы расчета можно приближенно вести на основе простейшей модели, использующей случай гладкой сферической поверхности Земли. В дальнейшем, на основе этой модели с некоторыми поправочными коэффициентами, учитывающими препятствия на протяжении трассы можно получить расчетные выражения для любых рельефов земной поверхности.

Экранирующее действие земной поверхности за счет ее кривизны ограничивает зону прямой видимости некоторым предельным расстоянием R_пр (рис. 6.1). Оно с учетом рефракции волны в атмосфере определяется из прямоугольных треугольников ACO и CBO, где прямая AB – касательная к земной поверхности в точке С.

получим 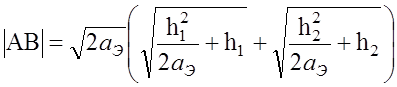             .       (6.1.3)

Учитывая, что  , длина траектории волны будет приближенно равна R_пр, а в выражении (6.1.3) можно будет пренебречь значением 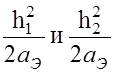.  С учетом рассмотренных приближений получим окончательное выражения для определения максимальной длины радиотрассы прямой видимости с учетом рефракции волны в атмосфере

.                            (6.1.4)

В дальнейшем принято условное разделение зон распространения радиоволн (см. рис. 6.1):

- на зону прямой видимости при ;

-зону полутени при ;

-зону тени при .

6.2. Множитель ослабления при распространении в зоне прямой видимости

Проанализируем влияние рельефа местности на напряженность поля в зоне прямой видимости. Оценка влияния в данном случае основана на простой модели интерференции прямой и отраженной от земной поверхности волн (рис. 6.2).

Рис. 6.2. К определению множителя ослабления при отражении

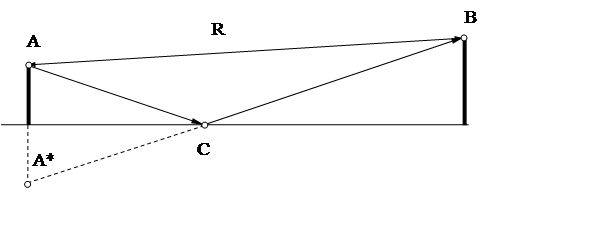от плоской поверхности

В данном случае происходит интерференция прямой и отраженной от земной поверхности  волн, отличающихся разностью хода и уровнем отраженной волны.

В результате напряженность поля в точке приема будет определятся выражением

,                              (6.2.1)

где - напряженность поля в точке приема прямой волны;

;

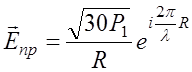– напряженность поля в точке приема для отраженной волны;

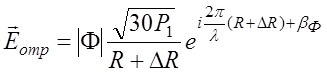,  в котором - разность хода отраженной и прямой волны;

 - модуль коэффициента отражения;

 - фазовый сдвиг, вызванный отражением от земной поверхности.

Подставив значения напряженностей поля в выражение (6.2.1), получим

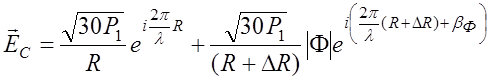.       (6.2.2)

Пологая, что для наземных трасс разность хода волн  достаточно мала, в результате она незначительно ослабляет уровень сигнала. Существенное влияние она оказывает только на фазовый сдвиг. Поэтому выражение (6.2.2) можно преобразовать в следующий вид

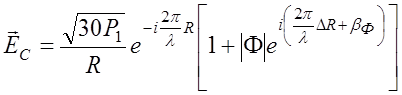,            (6.2.3)

откуда можно получить выражение для множителя ослабления

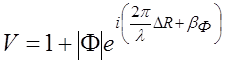.                         (6.2.4)

Из выражения (6.2.4) определим модуль множителя ослабления           

, где 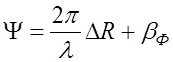, откуда после преобразований, получим окончательное выражение

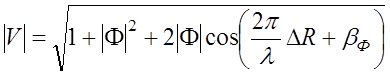.              (6.2.5)  

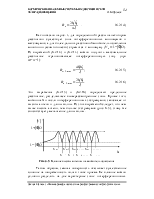
Проанализируем реальную трассу сферической формы (рис. 6.3).

В данной модели с учетом влияния сферичности поверхности Земли  коэффициент отражения будет меньше, чем от плоской поверхности. Для учета этого фактора используется коэффициент расходимости, определяемый выражением

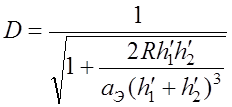,                            (6.2.6)

где  приведенные высоты поднятия антенн к плоскости, касательной к земной поверхности в точке C (cм. рис. 6.3);  a_Э – эквивалентный радиус  Земли, учитывающий явление рефракции в атмосфере.

В результате, в общем виде, выражение для модуля множителя ослабления  в случае сферической поверхности будет равно

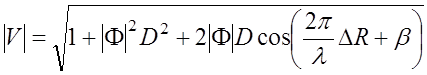.        (6.2.6)

Подкоренные значения в формуле (6.2.6) определяются из следующих выражений:

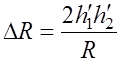;                                          (6.2.7)