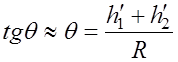Влияние рельефа местности на распространение УКВ. Причины ослабления напряженности поля поверхностных волн для случая гладкой сферической Земли, страница 2

;                                   (6.2.8)

;              ,          (6.2.9)

где

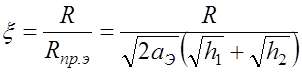.                    (6.2.10)

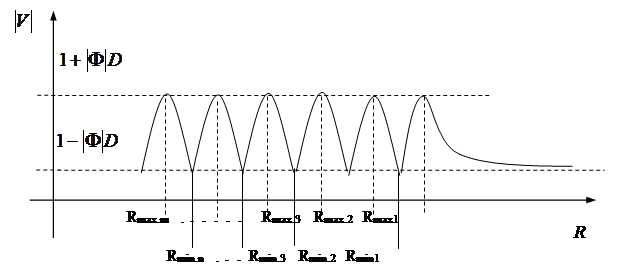
Анализируя значение множителя ослабления, можно заметить, что он имеет минимумы и максимумы, определяемые разностью хода прямой и отраженной волн , которая, в свою очередь, зависит от значений  (рис. 6.4).

 

Рис. 6.4. Зависимость множителя ослабления от расстояния

Ниже показано, что фазовый сдвиг при отражении от поверхности Земли , с учетом которого согласно формуле (6.2.6) максимумы множителя ослабления будут наблюдаться при

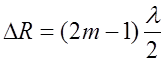,                               (6.2.11)

где m=1, 2, 3, … - номер максимума. Интерференционные минимумы будут наблюдаться при

,                                   (6.2.12)

где  n=1, 2, 3, … – номера интерференционного минимума. 

Значение модуля множителя ослабления для интерференционных максимумов и минимумов определяется из выражения (6.2.6) при соответствующих разностях хода волн -  .

Подставив в выражения (6.2.11) и (6.2.12) значение  из формулы (6.2.7), определим расстояния, соответствующие максимумам и минимумам множителя ослабления:

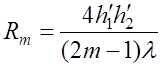;                                    (6.2.13)

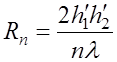
.                                       (6.2.14)

Как показано на рис. 4, для определенной трассы на некотором расстоянии существует зона интерференционных минимумов и максимумов, а для более дальних расстояний множитель ослабления монотонно (асимтотически) стремится к минимуму (). Из выражений (6.2.13) и (6.2.14) можно получить максимальное расстояние ограничивающее интерференционную зону (при m=n=1):

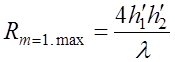;                                   (6.2.15)

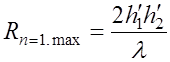.                                   (6.2.16)

Эти выражения (6.2.15) и (6.2.16) определяют предельное расстояние, разделяющее вышерассмотренные зоны. Кроме того, можно найти число интерференционных экстремумов, зависящее от высоты антенн и длины волны. Из этих выражений следует, что чем выше высота антенн, тем больше экстремумов (рис. 6.5), этому же способствует уменьшение длины волны.

 

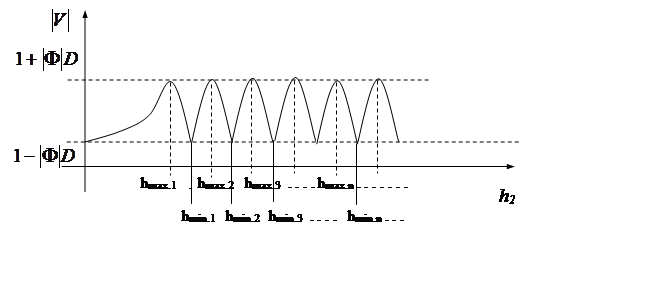Рис. 6.5.  Влияние высоты антенны на множитель ослабления

Таким образом, земная поверхность оказывает существенное влияние на напряженность поля в точке приема. Ее влияние можно условно разделить на две характерные зоны: интерференционных экстремумов и зону монотонного снижения уровня волны. При нахождении в зоне интерференционных экстремумов необходимо учитывать положение антенны для получения оптимальных характеристик образованного канала связи или телерадиовещания, за ее пределами уровень сигнала определяется только мощностью передающей станции и техническими характеристиками антенн.

6.3. Коэффициент отражения Земли и влияние на него

структуры неоднородностей

В рассмотренной модели для определения коэффициента отражения от земной поверхности с достаточной точностью можно воспользоваться френелевскими выражениями. Корректность применения таких выражений основана на приближенном использовании плоских волн в точке отражения, в силу достаточно больших расстояний до нее от передающей станции по сравнению с длиной волны (см. рис. 3).  С учетом достаточно малых значений углов падения и отражения , значения коэффициентов отражения определяется из следующих приближенных выражений:

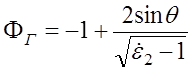;                                (6.3.1)

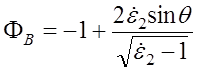,                                (6.3.2)

где  - диэлектрическая проницаемость Земли (с учетом ее проводимости   является комплексной величиной).   В случае, когда 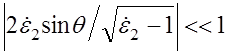 и 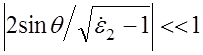 , что при малых углах  всегда выполняется, так как для земной поверхности .  В этом случае, для достаточно коротких волн, когда , , а          

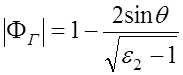;                                 (6.3.3)

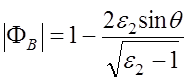.                                (6.3.4)

Здесь же следует заметить, что пользоваться вышерассмотренными выражениями коэффициентов отражения можно в случае, если Земля в зоне отражения имеет гладкую поверхность. Однако в реальных условиях не всегда это условие выполняется.

Отражательная способность Земли оценивается критерием Рэлея, который определяется высотой  неоднородностей в точке отражения:

,                                         (6.3.5)

который получается из оценки нарушения синфазности фронта отраженной волны, обусловленной рассеиванием электромагнитной энергии  неровностями (рис. 6.6).  Если 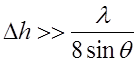, то рассеяние настолько велико, что отражением в зеркальном направлении можно пренебречь и интерференционная структура поля практически исчезает.

Рис. 6.6. К пояснению влияния неоднородностей Земли в точке отражения

Для оценки отражательной способности реальной земной поверхности необходимо проверять выполнение критерия Рэлея  в минимальной зоне вокруг точки отражения, которая получается в результате сечения эллипсоида минимальной области с фокусами в точке приема и вточке зеркального отображения источника относительно плоскости, касательной к Земле в геометрической точке отражения     (рис. 6.7). Эта зона имеет форму эллипса, центр  которого сдвинут от середины трассы на величину с_min, большая ось равна 2a_min, а малая ось – 2b_min, которые определяются из следующих выражений:

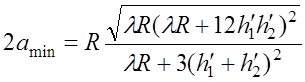;                           (6.3.6)

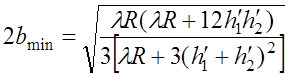.                             (6.3.7)

 

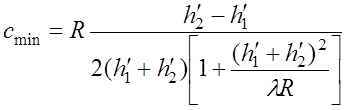;                   (6.3.18)

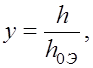
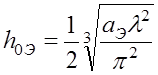        ;                  (6.4.4)

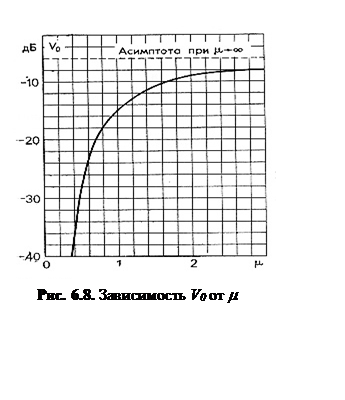
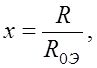
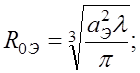                                                                (6.4.5)

Полученные выражения используются для инженерных расчетов на реальных трассах, с учетом рефракции волны в тропосфере, на которых нет существенных препятствий, значительно изменяющих кривизну поверхности Земли.