





















больше разность T1 −T0, тем большая доля теплоты, отбираемая от горячего источника, может быть превращена в работу в цикле.
Т.к. рабочее тело совершает замкнутый процесс, то его внутренняя энергия не изменяется и поэтому работа может быть совершена только за счёт Q1, сообщаемой рабочему телу горячим источником.
Eq не зависит от давления среды p0, т.к. Vостаётся неизменным; окружающая среда не подвергается в итоге сжатию или расширению и вся работа, произведённая рабочим телом за цикл, может быть использована по нашему усмотрению, т.к. является полезной.
Доля теплоты Q1, превращённой в работу в цикле, тем больше, чем выше термический КПД цикла.
Максимальная полезная работа некоторого количества теплоты Q1, отбираемой от горячего источника с температурой T1, будет получена в том случае, когда в рассматриваемой системе осуществляется обратимый цикл Карно. Следовательно:
Eq = Q1ηtо.ц.к = Q1(1− T0 ). (4.45)
T1
Если осуществить необратимый цикл, то полезная работа теплоты меньше чем Eq .
Любая необратимость приводит к уменьшению полезной работы. Полезная работа системы (или полезная работы теплоты) тем меньше, чем больше необратимость процессов, мерой которой является увеличением энтропии рассматриваемой изолированной системы. Поэтому между уменьшением полезной работы (или потерей эксергии) и возрастанием энтропии системы вследствие необратимости существует однозначная зависимость:
Eq −Lполез =T0[(S0// −S0/ )−(S−S0 )]=T0ΔSсист, (4.46) где ΔSсист − увеличение энтропии системы вследствие необратимости процесса.
Обозначим через D=(Eq − Lполез) – потерю эксергии системы.
Тогда уравнение (4.46) можно переписать в следующем виде:
D = T0ΔSсист. (4.47)
Уравнение (4.47) называют уравнением Гюи - Стодолы по имени французского физика М. Гюи, получившего это уравнение в 1889 г., и словацкого теплотехника А. Стодолы, впервые применившего это уравнение.
Мы получили максимальную полезную работу (эксергию) для любой изолированной системы, состоит из источника работы и среды. Это применимо для любых изолированных систем. Поскольку в большинстве тепловых и холодильных установках приходится иметь дело с непрерывным потоком рабочего тела для удобства анализа этих установок представляет целесообразным оперировать понятием эксергии системы для случая, когда процессы совершаются в потоке.
Рассмотрим неизолированную систему, состоящую из источника работы (источник рабочее тело с давлением P1 и T1) и окружающей среды (P0 и T0). Подсчитаем полезную максимальную работу (работа способность) источник работы (на единицу массы), при выводе используется путь, отличный от предыдущего.
Если источник работы имеет температуру T1 и давление p1, а среда
T0 и p0, то этот источник может быть переведён обратимо в состояние равновесия с окружающей средой следующим путём (см. рис. 4.4): в начале осуществляется обратимый адиабатный процесс, в результате которого температура источника снижена с T1 до T0, а давление от p1 до pa; затем осуществляется обратимый изотермический процесс, в котором за счёт теплообмена со средой источник работы достигает давления p0 (он обратим, т.к. температуры источников и среды в нём одинаковы и равна T0 и, следовательно, процесс теплообмена протекает при бесконечно малой разностью температур). Любой другой процесс был бы необратим.
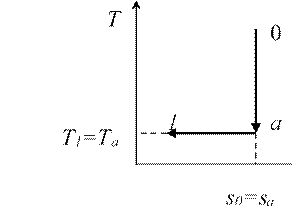
Рис. 4.4 К определению эксергии потока
Работа, совершаемая потоком в обратимом адиабатическом процессе 1а: l1обр−a = h1 − ha . (4.48)
Работа в изотермическом процессе
laобр−0 =(ha −h0)+ qa−0 , (4.49) где qa−0 − теплота, отводимая от источника работы (потока):
qa−0 =T0(Sa − S0), (4.50) и следовательно
laобр−0 = (ha −h0)+T0(Sa − S0). (4.51)
Поскольку
l1обр−0 = l1обр−a +laобр−0 , (4.52) и т.к. S1 =Sa, получим:
l1обр−0 = (h1 − h0) +T0(S0 − S1). (4.53)
Т.к. работа процесса обратимого изменения состояния источника работы представляет собой максимально полезную работу
(работоспособность), то
lполезмакс =(h1−h0)+T0(S0 −S1) (4.54)
Работоспособность потока называется эксергией потока:
e = (h − h0) +T0(S0 − S). (4.55)
Это понятие удобно для анализа теплосиловых установок и аппаратов.
Рассмотрим турбину. В турбину входит поток с параметрами p1,T1 выходит с параметрами p2,T2; внутри аппарата этот поток произвёл полезную работу lполез. Если процесс внутри аппарата необратим, то в аппарате имеет место потери эксергии d потока:
d = (e1 − e2) −lполез (4.56)
Если бы процесс в турбине был обратимый, то потеря работоспособности отсутствовали бы (d = 0) и в этом случае паток совершил бы максимально полезную работу:
lполезмакс = e1 −e2 (4.57)
В этом состоит основная идея эксергетического метода: рабочее тело входит в аппарат с эксергией e1 и совершает полезную работу lполез выходит из аппарата с e2; при этом потеря работоспособности вследствие необратимости процессов внутри аппарата определяется по уравнению
(4.56).
Эксергию можно рассматривать как своеобразную функцию состояния неравновесности системы, состоящей из окружающей среды и источников работы в виде потока.
По аналогии с эксергией потока рабочее тело используется, понятие об эксергии потока теплоты. Эксергия потока теплоты q, отдаваемой телом с температурой T , определяется следующим образом:
eq =
q(1− ![]() T ),
(4.58)
T ),
(4.58)
T0
где T0 − температура окружающей среды.
Если в тепловой аппарат, производящий полезную работу lполез входит
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.