











ГЛАВА 3 ТЕРМОДИНАМИКА ИДЕАЛЬНОГО ГАЗА.
СВОЙСТВА И ПРОЦЕССЫ
Введение понятия об идеальном газе позволило составить простые математические зависимости между величинами, характеризующими состояние тела, и на основе законов для идеальных газов создать стройную теорию термодинамических процессов.
Из молекулярно-кинетической теории газов следует, что абсолютное давление:
2 ![]() n
mw2
n
mw2
р=, (3.1)
3 v 2
где n − число молекул в удельном объёме;
![]()
![]() w
− средняя квадратичная скорость поступательного движения молекул; v − удельный
объём; m − масса молекулы ; mw2
w
− средняя квадратичная скорость поступательного движения молекул; v − удельный
объём; m − масса молекулы ; mw2
− средняя кинетическая энергия молекулы. 2
Кроме того, из молекулярно-кинетической теории
![]() mw2
mw2
=BT , (3.2)
2
гдеB − коэффициент пропорциональности. Тогда
pv =
![]() 2nBT .
(3.3)
2nBT .
(3.3)
3
Для двух состояний: р1V1 =![]() и р2V2 =
и р2V2 =![]() .
.
Почленное деление этих уравнений приводит к соотношению:
(p1v1)/T1 = (p2v2)/T2. (3.4)
Выражение (3.4) показывает, что произведение удельного объёма идеального газа на давление, делённое на абсолютную температуру для любого равновесного состояния есть величина постоянная – (pv)/T = const.
Постоянную величину обозначают R и называют удельной газовой постоянной.
(pv)/T = R или pv = RT . (3.5)
R зависит от природы газа и не зависит от его состояния.
Физический смысл удельной газовой постоянной:R [Дж/(кг·К)] − есть работа газа в процессе при p =const и при изменении температуры на один градус.
Итальянский учёный Авогадро в 1811 году доказал, что при одинаковых температурах и давлениях в равных объёмах различных идеальных газов содержится одинаковое количество молекул. Отсюда вытекает, что
v1M1 =v2M2, (3.6) где M1 и M2 – молекулярные массы газов.
![]() Молярная
масса М [кг/кмоль] − это отношение массы m системы к количеству газа
(вещества) v этой
системы.
Молярная
масса М [кг/кмоль] − это отношение массы m системы к количеству газа
(вещества) v этой
системы.
Произведение М ⋅v = v представляет собой объём одного моля газа, который при нормальных физических условиях равен 22,4 м3. Уравнение состояния для 1 моль газа:
![]()
pv = MRT , (3.7) где MR=Rμ = 8,314 Дж/(моль·К) − универсальная (молярная) газовая постоянная. Тогда
![]()
pv=RμT . (3.8)
Уравнение (3.8) называется уравнением Менделеева-Клапейрона.
3.2 Теплоёмкость идеального газа Ср, Сv.
Теплоемкость – это свойство тел поглощать и выделять теплоту при изменении температуры на один градус в различных термодинамических процессах. Различают среднюю и истинную теплоемкости.
Средняя теплоемкость – это отношение количества теплоты, полученной телом в термодинамическом процессе к разности температур в этом процессе:
![]()
C =
Q1−2 ![]() (t2
−t1),
[Дж/К]. (3.9)
(t2
−t1),
[Дж/К]. (3.9)
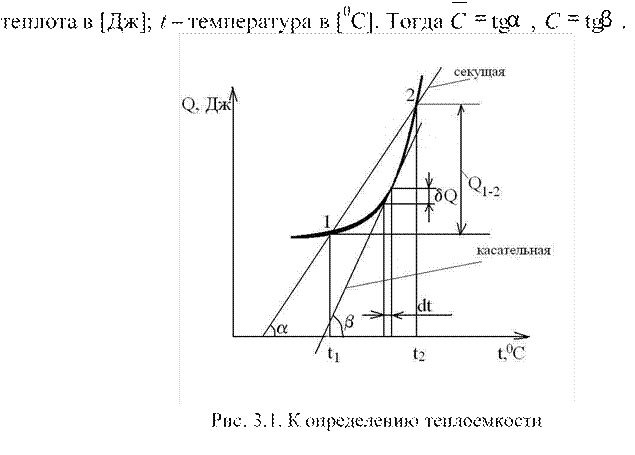
Истинная теплоемкость – это теплоемкость тела при бесконечном малом процессе:
С = dQ/dt, [Дж/К]. (3.10)
Рассмотрим произвольный термодинамический процесс 1-2 в координатах Q = f ( )t изображенный на рисунке 3.1, где Q – подведенная
Если термодинамическая система – однородное рабочее тело, то в расчетах применяются относительные теплоемкости:
- удельная массовая теплоемкость – теплоемкость, отнесенная к 1 кг вещества с = С/m, Дж/(кг·К);
- молярная теплоемкость – теплоемкость, отнесенная с 1 молю вещества Cˆ = C /n, Дж/(моль·К);
- объемная теплоемкость – теплоемкость, отнесенная к 1 м3 вещества С′ = С /V , Дж/(м3·К).
Теплоемкость – функция процесса и зависит от рода рабочего тела, характера процесса и параметров состояния. Так, теплоемкость в процессе с постоянным давлением называется изобарной теплоемкостью:
Сp = ∂Q = ∂H . (3.11)
∂T p ∂T p
Теплоемкость в процессе с постоянным объемом называется изохорной теплоемкостью:
СV = ∂Q = ∂U . (3.12)
∂T V ∂T V
Теплоемкость идеального газа не зависит от температуры и давления и зависит только от числа степеней свободы движения молекул и в соответствии с законом о равном распределении энергии по степеням свободы движения молекул теплоемкость:
СˆV = 3+δBp Rμ, (3.13)
2
где δBp - вращательные степени свободы, равные для одноатомного газа нулю (δBp = 0), для двухатомного газа - δBp=2 и для трехатомных газов δBp=3.
Теплоемкость реальных газов зависит от давления и температуры. В ряде случаев можно пренебречь влиянием давления на теплоемкость и принять, что теплоемкость реальных газов зависит только от температуры: C=f(t). Эта зависимость определяется экспериментально.
Для идеальных газов связь между изобарной и изохорной теплоёмкостями cp и cv устанавливается известным уравнением Майера:
cp −cv =R. (3.13)
Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе (v = const ) внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе ( p = const ) теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.
Для реальных газов cp −cv > R, так как при их расширении и p = const
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.