












ГЛАВА 2 ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Согласно закону сохранения и превращения энергии, являющимся наиболее общим законом природы, применимым ко всем явлениям и процессам, энергия изолированной системы (равная сумме всех видов энергии, имеющихся в системе) при любых происходящих в системе процессах не меняется; энергия не уничтожается и не создается.
Понятие энергии неразрывно связано с движением материи: энергия есть физическая мера движения материи, поэтому сохранение энергии выражает собой факт неуничтожимости движения материального мира. Существует и вторая формулировка: энергия – универсальная форма взаимодействия материи.
На основе закона сохранения и превращения энергии могут быть установлены точные количественные соотношения между отдельными видами энергии. Действительно, если различные виды энергии взяты в таких количествах, что каждое из них порознь вызывает одно и то же изменение состояния данной системы, то указанные количества энергии различных видов в силу взаимопревращаемости их будут являться эквивалентными.
Обозначим через Е общую энергию термодинамической системы независимо от конкретных форм, в которых она имеется в системе. Согласно закону сохранения и превращения энергии полная энергия изолированной системы не изменяется с течением времени, то есть E = const или E2 – E1 =
0.
В общем случае неизолированной термодинамический системы, находящейся в тепловом и механической взаимодействии с окружающими телами, изменение энергии системы будет связано с произведенной системой работой L и полученным системой количеством теплоты Q, вытекающим из закона сохранения и превращения энергии, соотношением:
E2 – E1 = Q – L (2.1)
Согласно этому уравнению, изменение энергии термодинамической системы равно разности между полученным системой количеством теплоты Q и совершенной ее работой L.
Внутренняя энергия. Любая термодинамическая система в каждом состоянии обладает запасом полной энергии E, которая состоит из внутренней энергии U , зависящей от внутреннего состояния тела, и внешней энергии Eвнеш., связанной с движением тела как целого и положением его в каком-либо внешнем поле сил (например в поле сил тяжести), т. е.
E U E= + внеш.. (2.2)
Если тело не движется, а влиянием внешнего поля сил можно пренебречь, то полная энергия будет представлять собой только внутреннюю энергию.
Любая термодинамическая система (рабочее тело) обладает запасом внутренней энергии, которая состоит из энергии хаотического (теплового) движения и взаимодействия молекул. Поскольку внутренняя энергия рабочего тела зависит от его массы, обычно пользуются значением внутренней энергии, отнесенной к 1 кг массы тела, – удельной внутренней энергией
u=U /m. (2.3)
В общем случае удельная кинетическая энергия теплового движения состоит из удельной кинетической энергии поступательного, вращательного и колебательного движений молекул, зависящей только от температуры рабочего тела, и удельной потенциальной энергии взаимодействия молекул между собой, которая, в свою очередь, зависит от среднего расстояния между молекулами, то есть от занимаемого рабочим телом объёма. Следовательно, в общем случае удельная внутренняя энергия рабочего тела зависит от его температуры T и удельного объема v, являясь однозначной функцией этих параметров состояния: u = f (T,v), или
du = ∂u ⋅dT + ∂u ⋅dv. (2.4)
∂T ∂v
Таким образом, важнейшим свойством удельной внутренней энергии рабочего тела является то, что она представляет собой однозначную функцию состояния тела, определяемого любой парой его основных параметров ( p, v, T ), и сама может служить параметром состояния. Из этого свойства следует, что изменение удельной внутренней энергии не зависит от характера процесса, а определяется лишь начальным и конечным состояниями рабочего тела.
В идеальном газе силы взаимодействия между молекулами отсутствуют и удельная потенциальная энергия его равна нулю. Поэтому удельная внутренняя энергия идеального газа состоит только из удельной кинетической энергии движения молекул Uкин и определяется его температурой:
u = f ( )T , или
du = ∂u ⋅dT. (2.5)
∂T
В замкнутом (круговом) процессе, в котором начальное и конечное состояния совпадают, изменение удельной внутренней энергии равно нулю.
Определять абсолютное значение удельной внутренней энергии в большинстве технических расчетов не требуется, так как обычно необходимо знать только ее изменение. Поэтому условно приписывают некоторому состоянию рабочего тела нулевое значение удельной внутренней энергии, а все расчеты ведут относительно этого значения.
Энтальпия. Рассмотрим полную энергию газа, находящегося под давлением p , создаваемым грузом массой M (рис. 2.1).
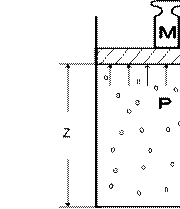
Рис 2.1. К определению энтальпии газа
В этом случае полная энергия E системы состоит из внутренней энергии газа U и потенциальной энергии груза, равной
M ⋅g ⋅z = p⋅ f ⋅z = p⋅V , (2.6)
где f - площадь поперечного сечения поршня.
То есть E =U + p⋅V . Величина pV , зависящая от сил, действующих на поршень, получила название потенциальной энергии давления. Таким образом, если газ находится в среде с давлением p, то с любым состоянием его связана некоторая энергия
U + pV = H , (2.7)
получившая название энтальпии газа в данном состоянии. Выражение энтальпии для 1 кг газа (т. е. удельной энтальпии) имеет вид:
h = u + pv (2.8)
Следовательно, удельная энтальпия, будучи зависимой от параметров состояния u, p, v также является параметром состояния. Поэтому изменение Δh, как и изменение Δu, не зависит от характера
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.