Последовательность разработки технической модели. Последовательность разработки технической модели

Содержание

Введение …………………………………………………………………….

1 Теоретические сведения

1.1Последовательность разработки технической модели……………...

1.2Применение численных методов в компьютерном                  моделировании …………………………………………………….…...….

1.3Численный метод Рунге-Кута и его применение в MathCad ……….

2 Алгоритмический анализ задачи

2.1 Полная постановка задачи…………………………………………...

2.2 Описание математической модели………………………………......

2.3Графическая схема алгоритма и её описание………………….…….

3 Описание реализации задачи в MathCAD

3.1 Описание реализации базовой модели в MathCAD ………………..

3.2 Описание реализации базовой модели в MathLAB…………………

3.3 Описание исследований в MathCAD ………………………………..

3.4 Выводы по результатам исследований………………………………

Заключение……………………………………………………………….....

Список использованных источников……………………………………

Приложение А. Реализация базовой модели в MathCad……………………………

Приложение Б. Решение дифференциального уравнения в MatLab……………...

Приложение В. Исследование…………………………………………………………..

Приложение Г. Нахождение аналитической и аппроксимирующей функций….

Введение

Научно-технический прогресс в современном мире развивается очень быстро. Эта быстрота характеризуется появлением новых видов техники, программного обеспечения, стандартных программ.

В последнее время появилось множество стандартных программ, которые значительно облегчают моделирование, и экономят время. Одной из таких программ является MathCAD.

Интегрированная система MathCAD предназначена для решения различного рода вычислительных задач, алгоритмы которых описываются в общепринятых математических терминах. Система имеет обширные вычислительные, графические, сервисные возможности, включает набор операторов программирования и ядро аналитического вычисления.

Система MathCAD является одной из самых мощных и эффективных математических направлений. Она ориентирована на широкий круг пользователей и позволяет выполнять математические расчёты, как в численном, так и в символьном аналитическом виде.

В данном курсовом проекте в среде MathCAD будет составлена математическая модель, а результаты моделирования будут представлены в виде расчетов и графиков.

-требует  информацию только  об одной  точке;

-имеет небольшую погрешность;

-значение функции  рассчитывается  при каждом шаге.

Формулы, описывающие классический метод Рунге-Кутта четвертого порядка, состоят из следующих пяти соотношений :

y_m+1=y_m+h/6(R₁+2R₂+2R₃+R₄)           (1.3.1)

где :

R₁=f(x_m,y_m)                                        (1.3.2)

R₂=f(x_m+h/2,y_m+hR₁/2)                      (1.3.3)

R₃=f(x_m+h/2,y_m+hR₂/2)                      (1.3.4)

R₄=f(x_m+h/2,y_m+hR₃/2)                      (1.3.5)     

Ошибка ограничения для этого метода равна e_t=kh 5 [3]            

Рисунок 2.2 - Схема алгоритма решения задачи

Описание графической схемы алгоритма:      1) Вводим исходные данные из таблицы 1 (п. 2.3).      2) Расчет и построение графика и  исходной функции гармонического воздействия e(t) , рисунок 2.1 (п. 2.2).      3) Рассчитываем значение функции напряжения на конденсаторе и времени в цепи с учётом гармонического воздействия e(t); производим построение графика этой  функций.      4) Затем решаем уравнение  (п.2.2), для каждого значения варьируемого параметра С.      5) Построение графиков зависимости u(t) для каждого варьируемого параметра.      6) Далее строим сводный график изменения всех значений варьируемого параметра С.      7) По полученным данным проводим аппроксимацию при помощи функции genfit и производим построение графиков.

Имея функцию, которой описывается напряжение, построил график зависимости  напряжения от времени (рисунок 3.1):

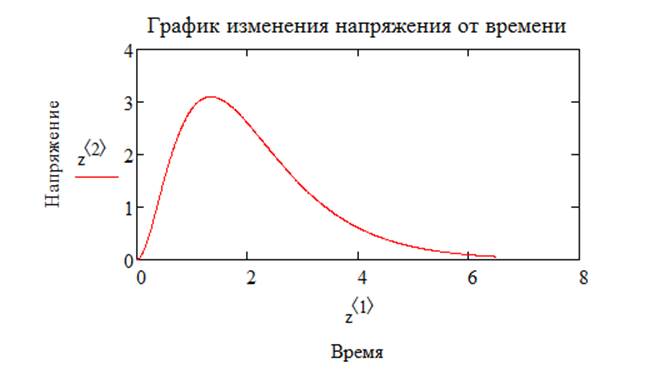
Рисунок 3.1 — график зависимости напряжения от времени

3.2 Описание реализации базовой модели в MathLAB

Технология решения дифференциальных уравнений в системе Matlab состоит в выполнении следующих шагов:

- создать вектор-функцию правых частей системы дифференциальных уравнений в виде М-файла;

- ввести функцию ode();

- получить решение нажатием клавиши Enter.

После нажатия клавиши на экране отобразится решение в виде таблицы с числом столбцов, равным числу неизвестных. Также система MATLAB позволяет получить график функции, являющейся решением. Для этого необходимо воспользоваться функцией plot(X, У).

Используя решатель ode45() (который имеет следующий синтаксис: ode45(‘<имя функции>‘, t0, tf, x0), где: ‘<имя функции>‘ – строковая переменная, являющаяся именем М-файла, в котором вычисляются правые части системы ОДУ; t0 – начальное значение времени; tf – конечное значение времени; x0 – вектор начальных условий)  пришли к решению, которое представлено в Приложении Б.

В результате получаются графики:

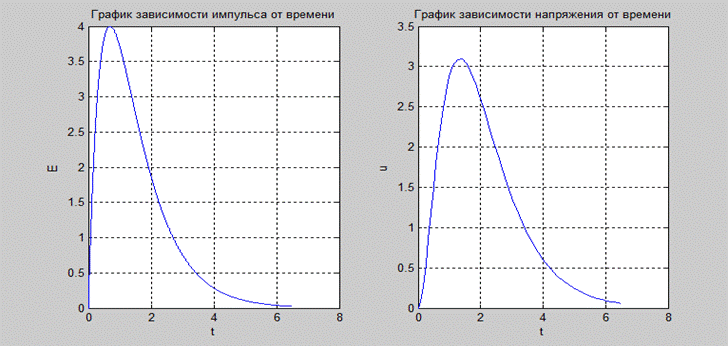
Рисунок 3.2.1 –  Графики зависимости импульса и  напряжения от времени, построенные в системе Matlab.

Построенные графики зависимости импульса и напряжения от времени в системе Matlab подтверждают правильность решения заданного дифференциального уравнения в системе MathCad.

3.3 Описание исследований в MathCAD

Воспользовавшись программной частью MathCad написал        программный