Защита уравнений. Нахождение значений функций

1.  Найти наибольшее (наименьшее) значение функции:

y(x)=-x²+4x-3

Найти корень уравнения y(x)=0.

Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.

2.  Найти наибольшее (наименьшее) значение функции:

Найти корень уравнения y(x)=0.

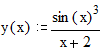Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.

3.  Найти наибольшее (наименьшее) значение функции:

Найти корень уравнения y(x)=0.

Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.

4.  Найти наибольшее (наименьшее) значение функции:

Найти корень уравнения y(x)=0.

Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.

5.  Найти наибольшее (наименьшее) значение функции:

Найти корень уравнения y(x)=0.

Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.

6.  Найти наибольшее (наименьшее) значение функции:

y(x)=-x²+4x-3

Найти корень уравнения y(x)=0.

Построить график функции с нанесением фоновых линий (маркеров) в точке максимума(минимума) и в точке, где функция обращается в 0.  Интервал изменения аргумента функции подобрать самостоятельно, исходя из полученных результатов.